Question Number 122448 by mohammad17 last updated on 17/Nov/20
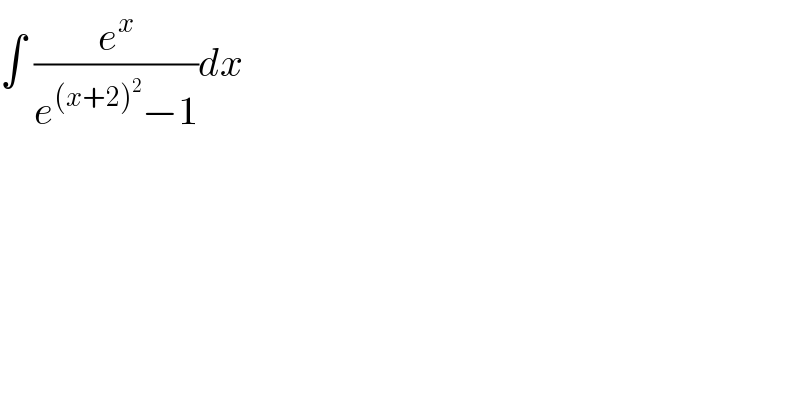
$$\int\:\frac{{e}^{{x}} }{{e}^{\left({x}+\mathrm{2}\right)^{\mathrm{2}} } −\mathrm{1}}{dx} \\ $$
Commented by mohammad17 last updated on 17/Nov/20

$${help}\:{me}\:{sir} \\ $$
Commented by MJS_new last updated on 17/Nov/20
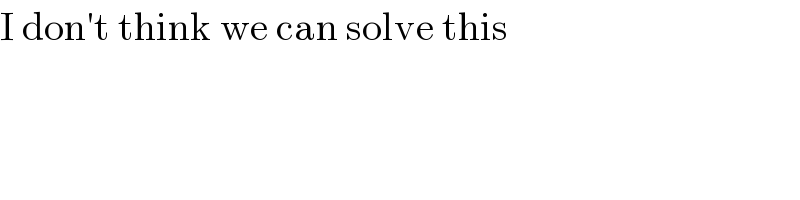
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20

$$\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\int\frac{{e}^{{t}} }{{e}^{{t}^{\mathrm{2}} } −\mathrm{1}}{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}={x}+\mathrm{2}\:\:\:\:\: \\ $$$$\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\int{e}^{{t}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{e}^{−{nt}^{\mathrm{2}} } {dt} \\ $$$$\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\int{e}^{−{nt}^{\mathrm{2}} +{t}} {dt}\:=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\int{e}^{−{n}\left(\left({t}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right)} {dt} \\ $$$$=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \int{e}^{−{n}\left({t}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)^{\mathrm{2}} } {dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({t}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)={u}\Rightarrow\mathrm{1}=\frac{{du}}{{dt}} \\ $$$$=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \int{e}^{−{nu}^{\mathrm{2}} } {du}\:\:\:\:\:\:\:\:\:\:\:\:{nu}^{\mathrm{2}} ={p}\Rightarrow\mathrm{2}{nu}=\frac{{dp}}{{du}} \\ $$$$=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \int\underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{nu}^{\mathrm{2}} \right)^{{k}} }{{k}!}{du} \\ $$$$=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{k}} }{{k}!}.\frac{{u}^{\mathrm{2}{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{1}}=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{k}} }{{k}!}.\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\left({x}−\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{2}\right)^{\mathrm{2}{k}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{k}} }{{k}!}.\frac{\left({x}−\frac{\mathrm{1}}{\mathrm{2}{n}}−\mathrm{2}\right)^{\mathrm{2}{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{1}}+\frac{{C}}{{e}^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}{e}^{\frac{\mathrm{1}}{\mathrm{4}{n}}} \underset{{k}\geqslant\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{n}\right)^{{k}} }{{k}!} \\ $$
