Question Number 115696 by Dwaipayan Shikari last updated on 27/Sep/20

Commented by Dwaipayan Shikari last updated on 27/Sep/20
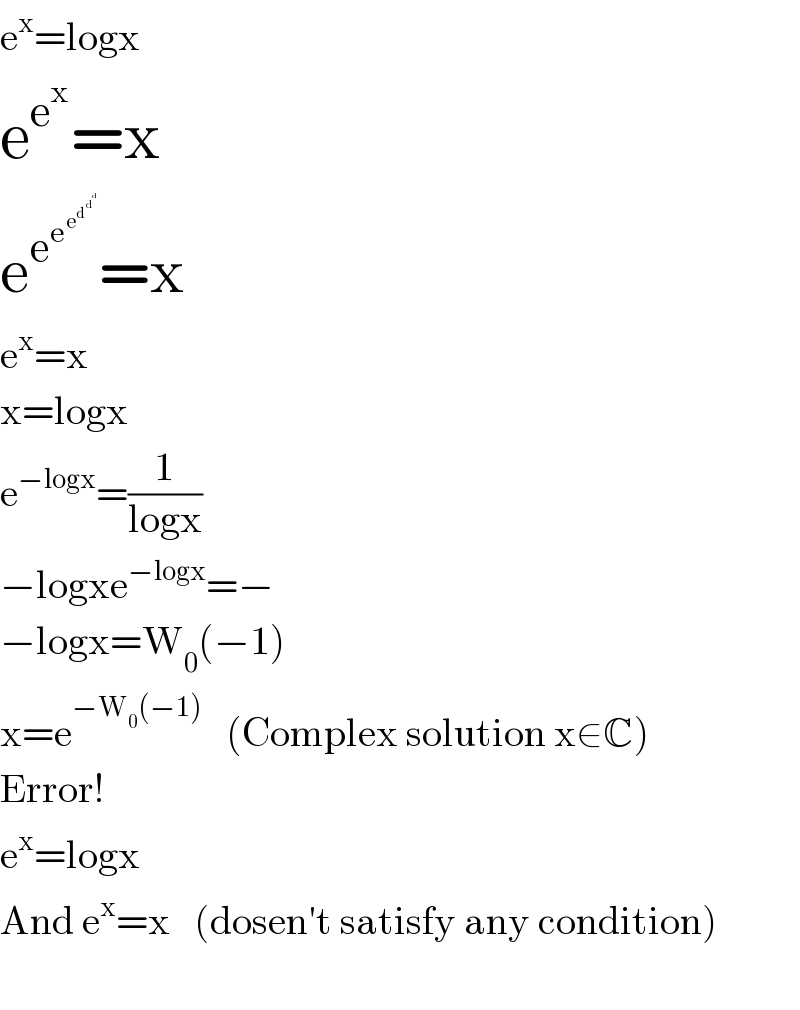
Commented by TANMAY PANACEA last updated on 27/Sep/20
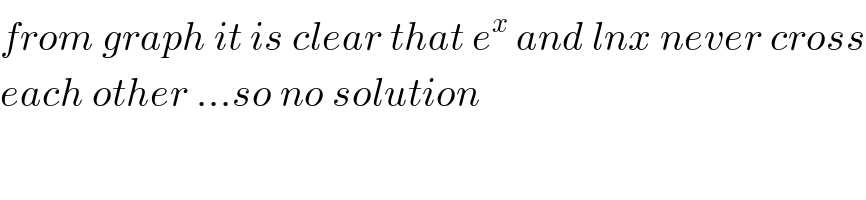
Commented by Dwaipayan Shikari last updated on 27/Sep/20
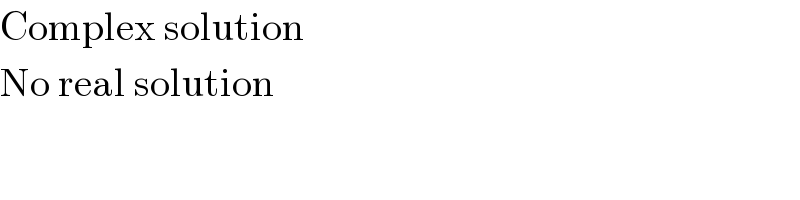
Commented by TANMAY PANACEA last updated on 27/Sep/20

