Question Number 166959 by cortano1 last updated on 03/Mar/22
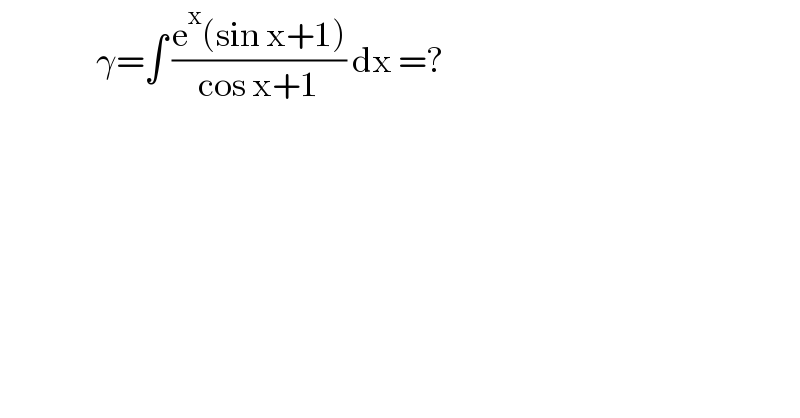
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\gamma=\int\:\frac{\mathrm{e}^{\mathrm{x}} \left(\mathrm{sin}\:\mathrm{x}+\mathrm{1}\right)}{\mathrm{cos}\:\mathrm{x}+\mathrm{1}}\:\mathrm{dx}\:=? \\ $$
Answered by ArielVyny last updated on 03/Mar/22
![γ=∫((e^x (sinx+1))/(cosx+1))dx t=tan((x/2))→2arctan(t)=x ∫e^(2arctant) ((((2t)/(1+t^2 ))+1)/(((1−t^2 )/(1+t^2 ))+1))×(2/(1+t^2 ))dt ∫e^(2arctag(t)) (((2t)/(1+t^2 ))+1)dt ∫(2/(1+t^2 ))e^(2arctg(t)) tdt+∫e^(2arctg(t)) dt du=(2/(1+t^2 ))e^(2arctg(t)) →u=e^(2arctg(t)) v=t→dv=1 [te^(2arctg(t)) ]−∫e^(2arctg(t)) dt+∫e^(2arctg(t)) dt =te^(2arctg(t)) γ=tan((x/2))e^x](https://www.tinkutara.com/question/Q166970.png)
$$\gamma=\int\frac{{e}^{{x}} \left({sinx}+\mathrm{1}\right)}{{cosx}+\mathrm{1}}{dx} \\ $$$${t}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow\mathrm{2}{arctan}\left({t}\right)={x} \\ $$$$\int{e}^{\mathrm{2}{arctant}} \frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{1}}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{1}}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\int{e}^{\mathrm{2}{arctag}\left({t}\right)} \left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{1}\right){dt} \\ $$$$\int\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{e}^{\mathrm{2}{arctg}\left({t}\right)} {tdt}+\int{e}^{\mathrm{2}{arctg}\left({t}\right)} {dt} \\ $$$${du}=\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{e}^{\mathrm{2}{arctg}\left({t}\right)} \rightarrow{u}={e}^{\mathrm{2}{arctg}\left({t}\right)} \\ $$$${v}={t}\rightarrow{dv}=\mathrm{1} \\ $$$$\left[{te}^{\mathrm{2}{arctg}\left({t}\right)} \right]−\int{e}^{\mathrm{2}{arctg}\left({t}\right)} {dt}+\int{e}^{\mathrm{2}{arctg}\left({t}\right)} {dt} \\ $$$$={te}^{\mathrm{2}{arctg}\left({t}\right)} \\ $$$$\gamma={tan}\left(\frac{{x}}{\mathrm{2}}\right){e}^{{x}} \\ $$$$ \\ $$
