Menu Close

e-x-sin-x-dx-e-x-cos-x-e-x-sin-x-e-x-sin-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 101212 by rb222 last updated on 01/Jul/20
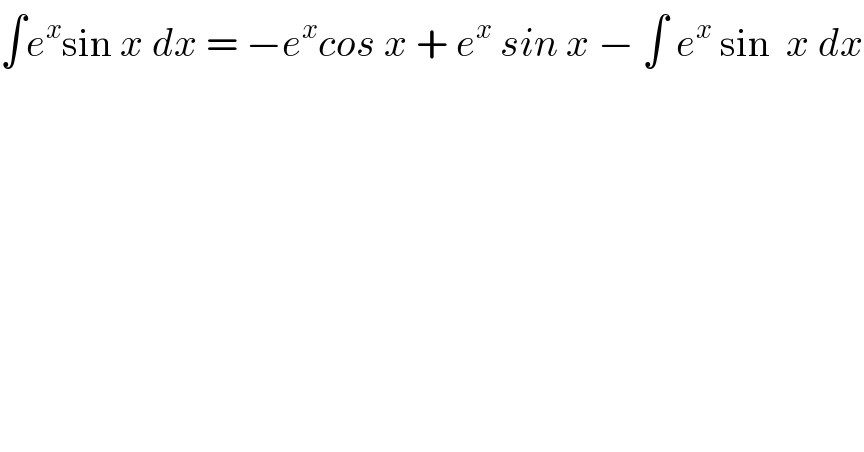
∫e^x sin x dx = −e^x cos x + e^x sin x − ∫ e^x sin x dx
$$\int{e}^{{x}} \mathrm{sin}\:{x}\:{dx}\:=\:−{e}^{{x}} {cos}\:{x}\:+\:{e}^{{x}} \:{sin}\:{x}\:−\:\int\:{e}^{{x}} \:\mathrm{sin}\:\:{x}\:{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
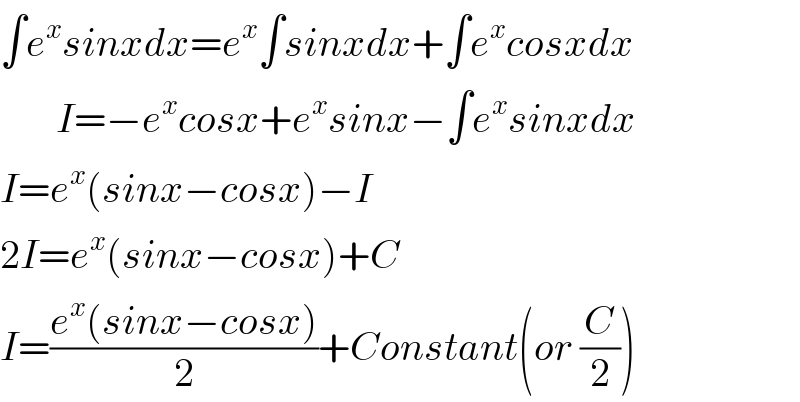
∫e^x sinxdx=e^x ∫sinxdx+∫e^x cosxdx I=−e^x cosx+e^x sinx−∫e^x sinxdx I=e^x (sinx−cosx)−I 2I=e^x (sinx−cosx)+C I=((e^x (sinx−cosx))/2)+Constant(or (C/2))
$$\int{e}^{{x}} {sinxdx}={e}^{{x}} \int{sinxdx}+\int{e}^{{x}} {cosxdx} \\ $$$$\:\:\:\:\:\:\:{I}=−{e}^{{x}} {cosx}+{e}^{{x}} {sinx}−\int{e}^{{x}} {sinxdx} \\ $$$${I}={e}^{{x}} \left({sinx}−{cosx}\right)−{I} \\ $$$$\mathrm{2}{I}={e}^{{x}} \left({sinx}−{cosx}\right)+{C} \\ $$$${I}=\frac{{e}^{{x}} \left({sinx}−{cosx}\right)}{\mathrm{2}}+{Constant}\left({or}\:\frac{{C}}{\mathrm{2}}\right) \\ $$
Answered by smridha last updated on 01/Jul/20
Im∫e^((1+i)x) dx=Im[(e^((1+i)x) /((1+i)))]+c =(1/2)Im[(1−i)e^x (cosx+isinx)]+c =(1/2)Im[e^x {(cosx+sinx)+i(sinx−cosx)}]+c =(e^x /2)(sinx−cosx)+c ans or =(e^x /( (√2)))(sinxcos(𝛑/4)−cosx.sin(𝛑/4))+c =(e^x /( (√2)))sin(x−(𝛑/4))+c ans or =(e^x /( (√2)))cos[(𝛑/2)+(x−(𝛑/4))]+c =(e^x /( (√2)))cos[x+(𝛑/4)]+c ans let I=∫e^x sinx=e^x sinx−∫e^x cosx =e^x sinx−e^x cosx−∫e^x sinx =e^x (sinx−cosx)−I+k 2I=e^x (sinx−cosx)+k so I=(e^x /2)(sinx−cosx)+c [c=(k/2)=constant]
$$\boldsymbol{{Im}}\int\boldsymbol{{e}}^{\left(\mathrm{1}+\boldsymbol{{i}}\right)\boldsymbol{{x}}} \boldsymbol{{dx}}=\boldsymbol{{I}}{m}\left[\frac{\boldsymbol{{e}}^{\left(\mathrm{1}+\boldsymbol{{i}}\right)\boldsymbol{{x}}} }{\left(\mathrm{1}+\boldsymbol{{i}}\right)}\right]+\boldsymbol{{c}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{I}}{m}\left[\left(\mathrm{1}−\boldsymbol{{i}}\right)\boldsymbol{{e}}^{\boldsymbol{{x}}} \left(\boldsymbol{{cosx}}+\boldsymbol{{isinx}}\right)\right]+\boldsymbol{{c}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{I}}{m}\left[\boldsymbol{{e}}^{\boldsymbol{{x}}} \left\{\left(\boldsymbol{{cosx}}+\boldsymbol{{sinx}}\right)+\boldsymbol{{i}}\left(\boldsymbol{{sinx}}−\boldsymbol{{cosx}}\right)\right\}\right]+\boldsymbol{{c}} \\ $$$$=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\mathrm{2}}\left(\boldsymbol{{sinx}}−\boldsymbol{{cosx}}\right)+\boldsymbol{{c}}\:\:\:\:\:\boldsymbol{{ans}} \\ $$$$\boldsymbol{{or}}\:=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\:\sqrt{\mathrm{2}}}\left(\boldsymbol{{sinxcos}}\frac{\boldsymbol{\pi}}{\mathrm{4}}−\boldsymbol{{cosx}}.\boldsymbol{{sin}}\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)+\boldsymbol{{c}} \\ $$$$\:\:\:=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\:\sqrt{\mathrm{2}}}\boldsymbol{{sin}}\left(\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)+\boldsymbol{{c}}\:\:\:\:\:\:\:\:\boldsymbol{{ans}} \\ $$$$\boldsymbol{{or}}\:=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\:\sqrt{\mathrm{2}}}\boldsymbol{{cos}}\left[\frac{\boldsymbol{\pi}}{\mathrm{2}}+\left(\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)\right]+\boldsymbol{{c}} \\ $$$$\:\:\:\:=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\:\sqrt{\mathrm{2}}}\boldsymbol{{cos}}\left[\boldsymbol{{x}}+\frac{\boldsymbol{\pi}}{\mathrm{4}}\right]+\boldsymbol{{c}}\:\:\:\:\:\:\:\:\boldsymbol{{ans}} \\ $$$$\boldsymbol{{let}}\:\:\: \\ $$$$\boldsymbol{{I}}=\int\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{sinx}}=\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{sinx}}−\int\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{cosx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{sinx}}−\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{cosx}}−\int\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{sinx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{e}}^{\boldsymbol{{x}}} \left(\boldsymbol{{sinx}}−\boldsymbol{{cosx}}\right)−\boldsymbol{{I}}+\boldsymbol{{k}} \\ $$$$\mathrm{2}\boldsymbol{{I}}=\boldsymbol{{e}}^{\boldsymbol{{x}}} \left(\boldsymbol{{sinx}}−\boldsymbol{{cosx}}\right)+\boldsymbol{{k}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}} }{\mathrm{2}}\left(\boldsymbol{{sinx}}−\boldsymbol{{cosx}}\right)+\boldsymbol{{c}}\:\:\:\:\left[\boldsymbol{{c}}=\frac{\boldsymbol{{k}}}{\mathrm{2}}=\boldsymbol{{constant}}\right] \\ $$
Commented by smridha last updated on 01/Jul/20
who are you man ??well copied!!
$$\boldsymbol{{who}}\:\boldsymbol{{are}}\:\boldsymbol{{you}}\:\boldsymbol{{man}}\:??\boldsymbol{{well}}\:\boldsymbol{{copied}}!! \\ $$
Answered by MJS last updated on 01/Jul/20
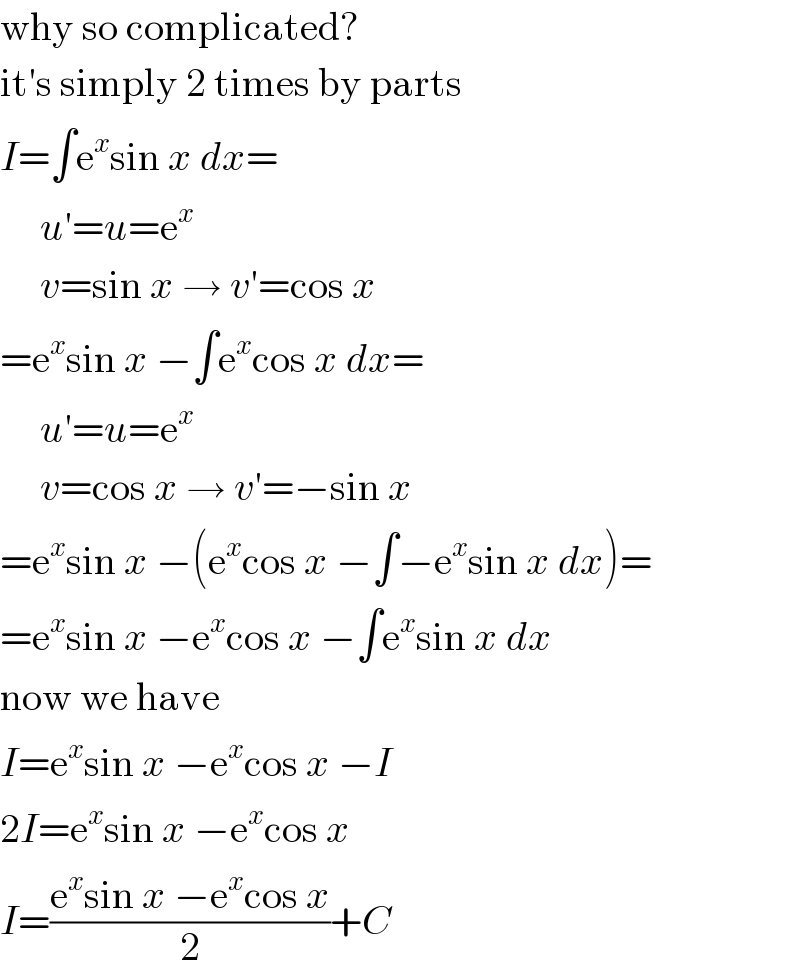
why so complicated? it′s simply 2 times by parts I=∫e^x sin x dx= u′=u=e^x v=sin x → v′=cos x =e^x sin x −∫e^x cos x dx= u′=u=e^x v=cos x → v′=−sin x =e^x sin x −(e^x cos x −∫−e^x sin x dx)= =e^x sin x −e^x cos x −∫e^x sin x dx now we have I=e^x sin x −e^x cos x −I 2I=e^x sin x −e^x cos x I=((e^x sin x −e^x cos x)/2)+C
$$\mathrm{why}\:\mathrm{so}\:\mathrm{complicated}? \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{simply}\:\mathrm{2}\:\mathrm{times}\:\mathrm{by}\:\mathrm{parts} \\ $$$${I}=\int\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:{dx}= \\ $$$$\:\:\:\:\:{u}'={u}=\mathrm{e}^{{x}} \\ $$$$\:\:\:\:\:{v}=\mathrm{sin}\:{x}\:\rightarrow\:{v}'=\mathrm{cos}\:{x} \\ $$$$=\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:−\int\mathrm{e}^{{x}} \mathrm{cos}\:{x}\:{dx}= \\ $$$$\:\:\:\:\:{u}'={u}=\mathrm{e}^{{x}} \\ $$$$\:\:\:\:\:{v}=\mathrm{cos}\:{x}\:\rightarrow\:{v}'=−\mathrm{sin}\:{x} \\ $$$$=\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:−\left(\mathrm{e}^{{x}} \mathrm{cos}\:{x}\:−\int−\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:{dx}\right)= \\ $$$$=\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:−\mathrm{e}^{{x}} \mathrm{cos}\:{x}\:−\int\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:{dx} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$${I}=\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:−\mathrm{e}^{{x}} \mathrm{cos}\:{x}\:−{I} \\ $$$$\mathrm{2}{I}=\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:−\mathrm{e}^{{x}} \mathrm{cos}\:{x} \\ $$$${I}=\frac{\mathrm{e}^{{x}} \mathrm{sin}\:{x}\:−\mathrm{e}^{{x}} \mathrm{cos}\:{x}}{\mathrm{2}}+{C} \\ $$
Commented by smridha last updated on 02/Jul/20
����������������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *