Question Number 23108 by Kathie last updated on 26/Oct/17
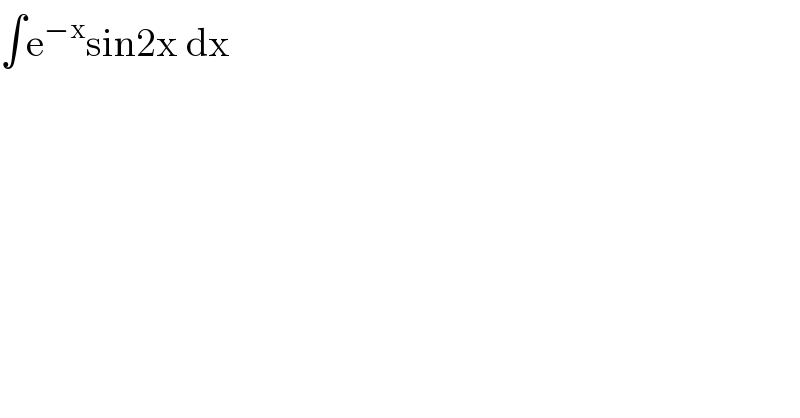
$$\int\mathrm{e}^{−\mathrm{x}} \mathrm{sin2x}\:\mathrm{dx} \\ $$
Answered by sma3l2996 last updated on 26/Oct/17
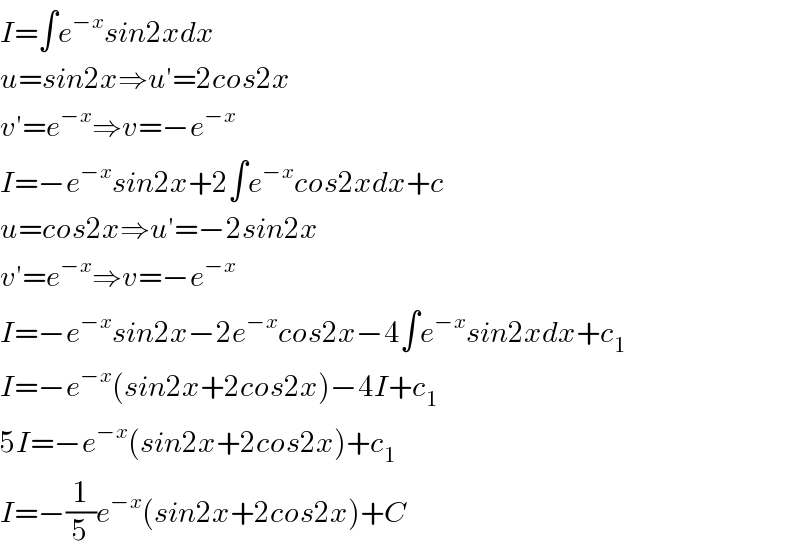
$${I}=\int{e}^{−{x}} {sin}\mathrm{2}{xdx} \\ $$$${u}={sin}\mathrm{2}{x}\Rightarrow{u}'=\mathrm{2}{cos}\mathrm{2}{x} \\ $$$${v}'={e}^{−{x}} \Rightarrow{v}=−{e}^{−{x}} \\ $$$${I}=−{e}^{−{x}} {sin}\mathrm{2}{x}+\mathrm{2}\int{e}^{−{x}} {cos}\mathrm{2}{xdx}+{c} \\ $$$${u}={cos}\mathrm{2}{x}\Rightarrow{u}'=−\mathrm{2}{sin}\mathrm{2}{x} \\ $$$${v}'={e}^{−{x}} \Rightarrow{v}=−{e}^{−{x}} \\ $$$${I}=−{e}^{−{x}} {sin}\mathrm{2}{x}−\mathrm{2}{e}^{−{x}} {cos}\mathrm{2}{x}−\mathrm{4}\int{e}^{−{x}} {sin}\mathrm{2}{xdx}+{c}_{\mathrm{1}} \\ $$$${I}=−{e}^{−{x}} \left({sin}\mathrm{2}{x}+\mathrm{2}{cos}\mathrm{2}{x}\right)−\mathrm{4}{I}+{c}_{\mathrm{1}} \\ $$$$\mathrm{5}{I}=−{e}^{−{x}} \left({sin}\mathrm{2}{x}+\mathrm{2}{cos}\mathrm{2}{x}\right)+{c}_{\mathrm{1}} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{5}}{e}^{−{x}} \left({sin}\mathrm{2}{x}+\mathrm{2}{cos}\mathrm{2}{x}\right)+{C} \\ $$
