Question Number 95405 by i jagooll last updated on 25/May/20
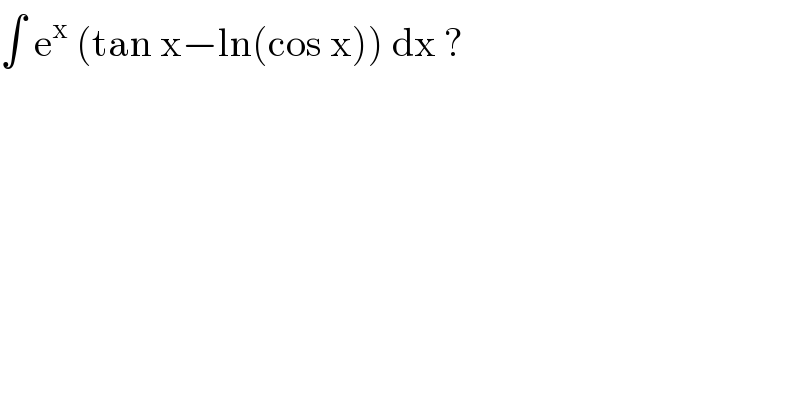
$$\int\:\mathrm{e}^{\mathrm{x}} \:\left(\mathrm{tan}\:\mathrm{x}−\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)\:\mathrm{dx}\:? \\ $$
Commented by PRITHWISH SEN 2 last updated on 25/May/20

$$\mathrm{yes} \\ $$
Commented by bobhans last updated on 25/May/20

$$\mathrm{no}.\:−\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\:+\:\mathrm{c}\: \\ $$$$\mathrm{or}\:\mathrm{e}^{\mathrm{x}} \:\mathrm{ln}\left(\mathrm{sec}\:\mathrm{x}\right)\:+\:\mathrm{c} \\ $$
Commented by bobhans last updated on 25/May/20

$$\frac{\mathrm{d}}{\mathrm{dx}}\:\left(\mathrm{e}^{\mathrm{x}} \:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)\:=\:\mathrm{e}^{\mathrm{x}} \:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\:+\:\frac{\mathrm{e}^{\mathrm{x}} \left(−\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{cos}\:\mathrm{x}} \\ $$$$=\:\mathrm{e}^{\mathrm{x}} \:\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\:−\mathrm{e}^{\mathrm{x}} \:\mathrm{tan}\:\left(\mathrm{x}\right)\:\neq\:\mathrm{with}\:\mathrm{equation} \\ $$
Answered by bobhans last updated on 25/May/20
![∫(tan x−ln(cos x)) d(e^x ) =I u = tan x−ln(cos x)) du = sec^2 x+tan x dx I = e^x (tan x−ln(cos x))−∫ e^x (sec^2 x+tan x) dx I= e^x (tan x−ln(cos x))−∫e^x d(tan x)−∫e^x tan x dx I= e^x (tan x−ln(cos x))−[ e^x tan x−∫e^x tan x dx ]−∫e^x tan x dx I= e^x tan x−e^x ln(cos x))−e^x tan x + c I = e^x ln(sec x) + c](https://www.tinkutara.com/question/Q95407.png)
$$\int\left(\mathrm{tan}\:\mathrm{x}−\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)\:\mathrm{d}\left(\mathrm{e}^{\mathrm{x}} \right)\:=\mathrm{I} \\ $$$$\left.\mathrm{u}\:=\:\mathrm{tan}\:\mathrm{x}−\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right) \\ $$$$\mathrm{du}\:=\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:\mathrm{x}\:\mathrm{dx}\: \\ $$$$\mathrm{I}\:=\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{tan}\:\mathrm{x}−\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)−\int\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:\mathrm{dx} \\ $$$$\mathrm{I}=\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{tan}\:\mathrm{x}−\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)−\int\mathrm{e}^{\mathrm{x}} \:\mathrm{d}\left(\mathrm{tan}\:\mathrm{x}\right)−\int\mathrm{e}^{\mathrm{x}} \mathrm{tan}\:\mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{I}=\:\mathrm{e}^{\mathrm{x}} \left(\mathrm{tan}\:\mathrm{x}−\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)−\left[\:\mathrm{e}^{\mathrm{x}} \:\mathrm{tan}\:\mathrm{x}−\int\mathrm{e}^{\mathrm{x}} \mathrm{tan}\:\mathrm{x}\:\mathrm{dx}\:\right]−\int\mathrm{e}^{\mathrm{x}} \mathrm{tan}\:\mathrm{x}\:\mathrm{dx} \\ $$$$\left.\mathrm{I}=\:\mathrm{e}^{\mathrm{x}} \mathrm{tan}\:\mathrm{x}−\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\right)−\mathrm{e}^{\mathrm{x}} \:\mathrm{tan}\:\mathrm{x}\:+\:\mathrm{c}\: \\ $$$$\mathrm{I}\:=\:\mathrm{e}^{\mathrm{x}} \:\mathrm{ln}\left(\mathrm{sec}\:\mathrm{x}\right)\:+\:\mathrm{c}\: \\ $$
Commented by i jagooll last updated on 25/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{bob} \\ $$
