Question Number 111010 by mohammad17 last updated on 01/Sep/20
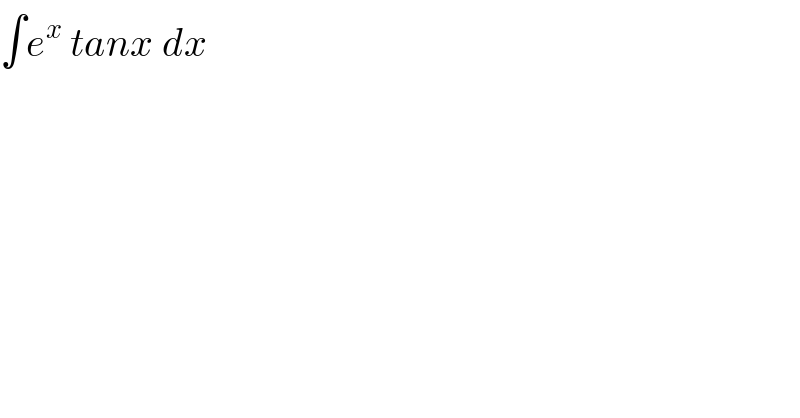
$$\int{e}^{{x}} \:{tanx}\:{dx} \\ $$
Answered by Rio Michael last updated on 02/Sep/20

$$\mathrm{Let}\:\mathrm{me}\:\mathrm{try}\:\mathrm{this},\:\mathrm{it}'\mathrm{s}\:\:\mathrm{something}\:\mathrm{i}\:\mathrm{learnt} \\ $$$$\mathrm{on}\:\mathrm{my}\:\mathrm{own}. \\ $$$$\mathrm{Let}\:{I}\:=\:\int\:{e}^{{x}} \:\mathrm{tan}\:{x}\:{dx}. \\ $$$$\mathrm{we}\:\mathrm{define}\:\mathrm{tan}\:{x}\:=\:−{i}\:\frac{\mathrm{1}−{e}^{−\mathrm{2}{ix}} }{\mathrm{1}\:+\:{e}^{−\mathrm{2}{ix}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−{i}−\mathrm{2}{i}\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{r}} {e}^{−\mathrm{2}{irx}} \\ $$$$\mathrm{so},\:\int{e}^{{x}} \:\mathrm{tan}\:{x}\:{dx}\:=−{ie}^{{x}} −\mathrm{2}{i}\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{r}} \int{e}^{\left(\mathrm{1}−\mathrm{2}{ir}\right){x}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−{ie}^{{x}} \:−\mathrm{2}{i}\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} }{\mathrm{1}−\mathrm{2}{ir}}{e}^{\left(\mathrm{1}−\mathrm{2}{ir}\right){x}} \:+\:{k}\:\left(\mathrm{a}\:\mathrm{constant}\right) \\ $$$$\mathrm{am}\:\mathrm{sorry}\:\mathrm{but}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{involves}\:\mathrm{the}\:{L}\mathrm{erch}\:{P}\mathrm{hi}\:\mathrm{function}\:\mathrm{which} \\ $$$$\mathrm{i}\:\mathrm{have}\:\mathrm{no}\:\mathrm{understanding}\:\mathrm{of}\:\mathrm{it}\:\mathrm{till}\:\mathrm{today}. \\ $$
