Question Number 129275 by abdurehime last updated on 14/Jan/21
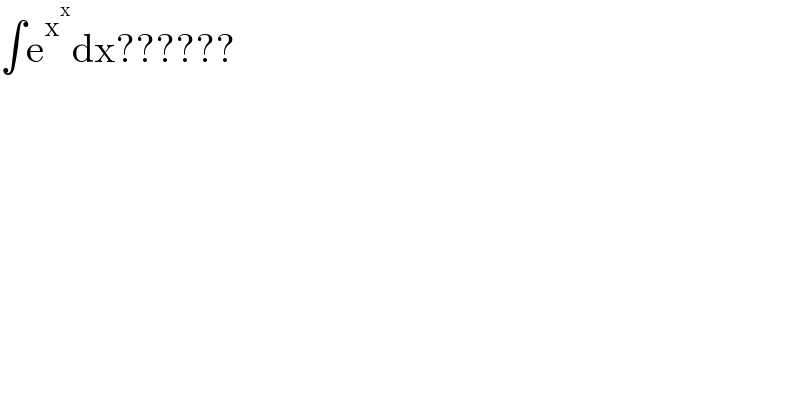
$$\int\mathrm{e}^{\mathrm{x}^{\mathrm{x}} } \mathrm{dx}?????? \\ $$
Commented by abdurehime last updated on 14/Jan/21

$$\mathrm{no}\:\mathrm{one}???? \\ $$
Commented by Dwaipayan Shikari last updated on 14/Jan/21
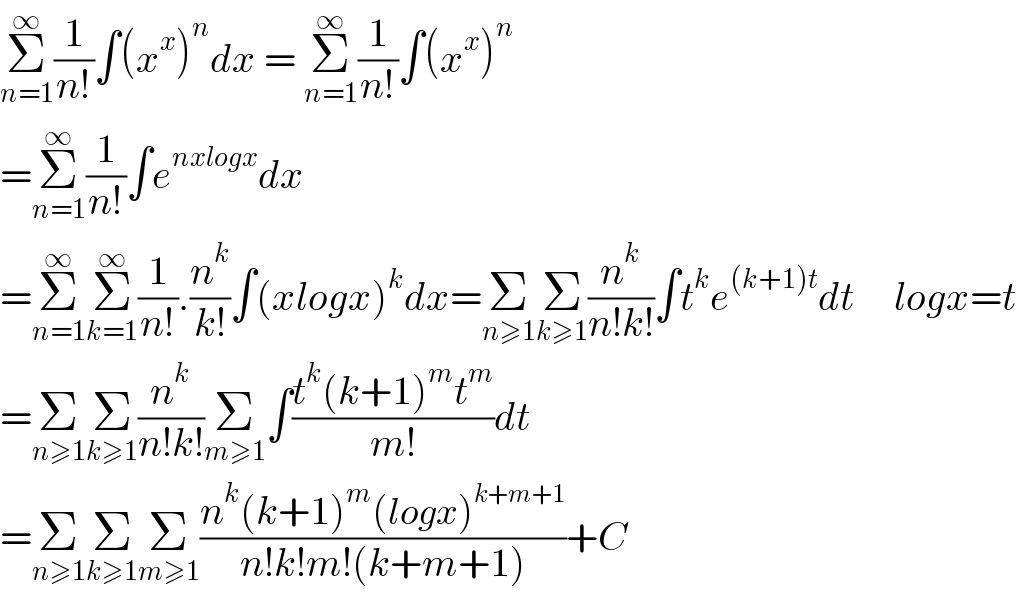
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int\left({x}^{{x}} \right)^{{n}} {dx}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int\left({x}^{{x}} \right)^{{n}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int{e}^{{nxlogx}} {dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}.\frac{{n}^{{k}} }{{k}!}\int\left({xlogx}\right)^{{k}} {dx}=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{n}^{{k}} }{{n}!{k}!}\int{t}^{{k}} {e}^{\left({k}+\mathrm{1}\right){t}} {dt}\:\:\:\:\:{logx}={t} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{n}^{{k}} }{{n}!{k}!}\underset{{m}\geqslant\mathrm{1}} {\sum}\int\frac{{t}^{{k}} \left({k}+\mathrm{1}\right)^{{m}} {t}^{{m}} }{{m}!}{dt} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}\geqslant\mathrm{1}} {\sum}\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{{n}^{{k}} \left({k}+\mathrm{1}\right)^{{m}} \left({logx}\right)^{{k}+{m}+\mathrm{1}} }{{n}!{k}!{m}!\left({k}+{m}+\mathrm{1}\right)}+{C} \\ $$
