Question Number 149252 by holomata last updated on 04/Aug/21
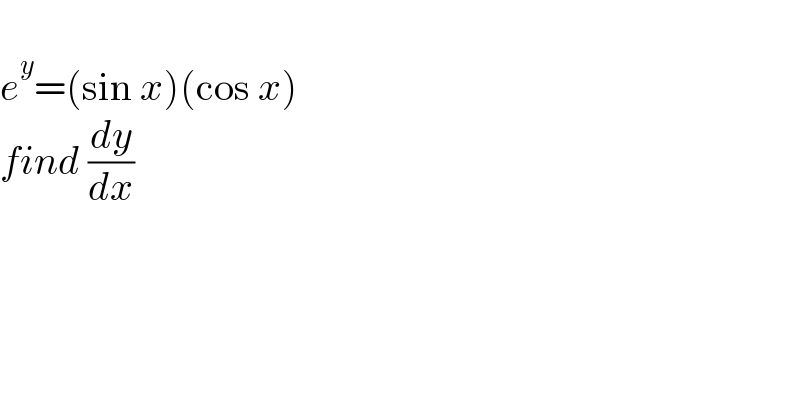
$$ \\ $$$${e}^{{y}} =\left(\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}\right) \\ $$$${find}\:\frac{{dy}}{{dx}} \\ $$
Answered by Mokmokhi last updated on 04/Aug/21

$$\frac{{dy}}{{dx}}=\mathrm{2cot}\:\mathrm{2}{x} \\ $$
Answered by physicstutes last updated on 04/Aug/21
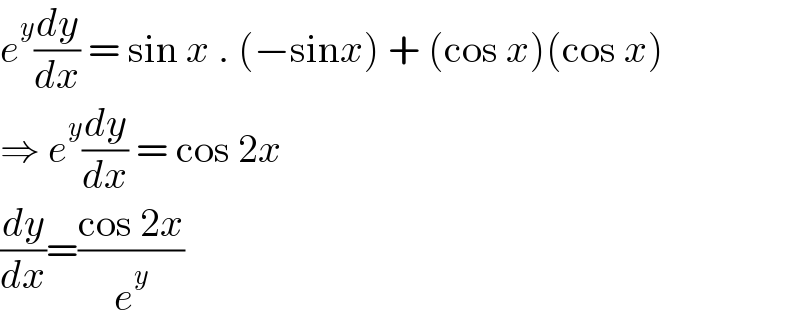
$${e}^{{y}} \frac{{dy}}{{dx}}\:=\:\mathrm{sin}\:{x}\:.\:\left(−\mathrm{sin}{x}\right)\:+\:\left(\mathrm{cos}\:{x}\right)\left(\mathrm{cos}\:{x}\right) \\ $$$$\Rightarrow\:{e}^{{y}} \frac{{dy}}{{dx}}\:=\:\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{cos}\:\mathrm{2}{x}}{{e}^{{y}} } \\ $$
Commented by Mokmokhi last updated on 04/Aug/21
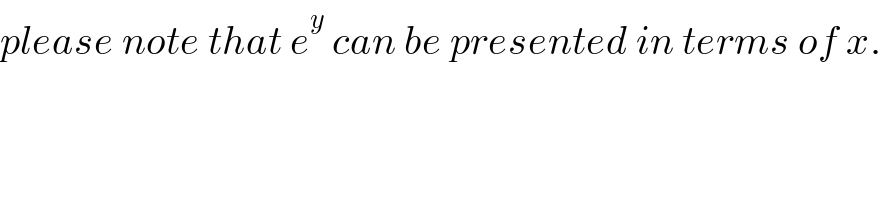
$${please}\:{note}\:{that}\:{e}^{{y}} \:{can}\:{be}\:{presented}\:{in}\:{terms}\:{of}\:{x}. \\ $$
Answered by puissant last updated on 04/Aug/21
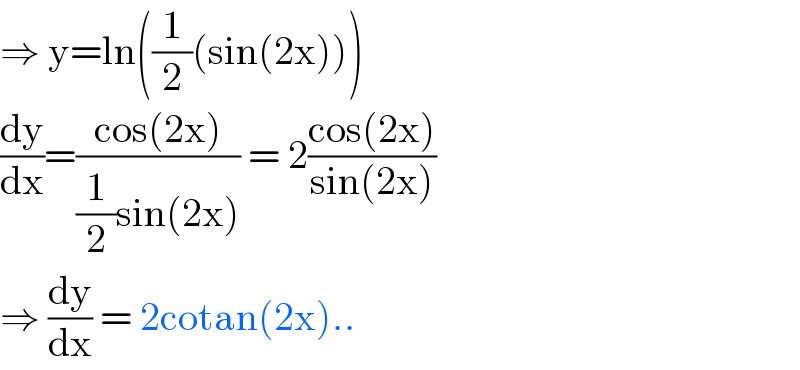
$$\Rightarrow\:\mathrm{y}=\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)\right) \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)}\:=\:\mathrm{2}\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{sin}\left(\mathrm{2x}\right)} \\ $$$$\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{2cotan}\left(\mathrm{2x}\right).. \\ $$
Answered by mathmax by abdo last updated on 04/Aug/21
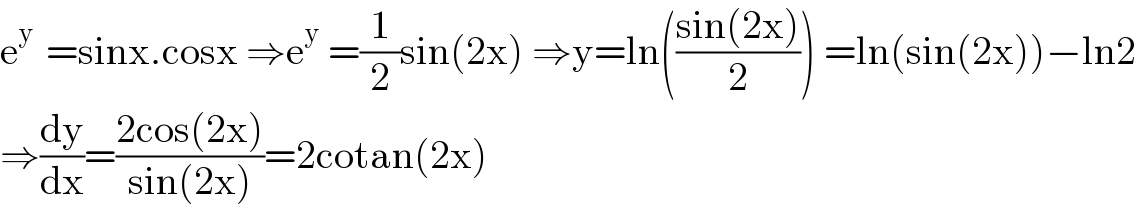
$$\mathrm{e}^{\mathrm{y}\:} \:=\mathrm{sinx}.\mathrm{cosx}\:\Rightarrow\mathrm{e}^{\mathrm{y}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\:\Rightarrow\mathrm{y}=\mathrm{ln}\left(\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\:=\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)−\mathrm{ln2} \\ $$$$\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{2cos}\left(\mathrm{2x}\right)}{\mathrm{sin}\left(\mathrm{2x}\right)}=\mathrm{2cotan}\left(\mathrm{2x}\right) \\ $$
