Question Number 88417 by M±th+et£s last updated on 10/Apr/20
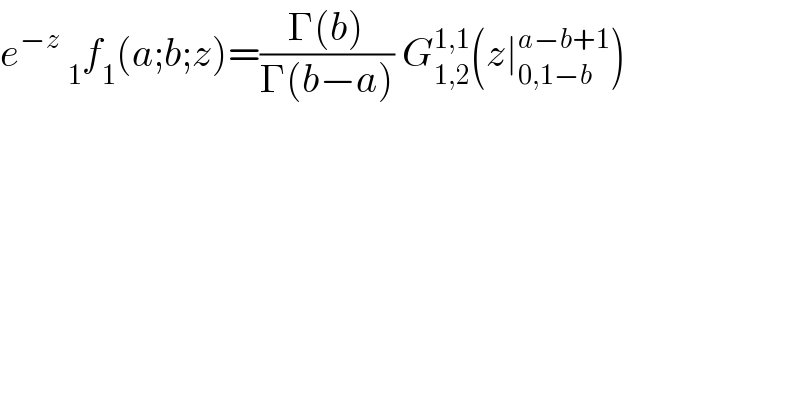
$${e}^{−{z}} \:_{\mathrm{1}} {f}_{\mathrm{1}} \left({a};{b};{z}\right)=\frac{\Gamma\left({b}\right)}{\Gamma\left({b}−{a}\right)}\:{G}_{\mathrm{1},\mathrm{2}} ^{\mathrm{1},\mathrm{1}} \left({z}\mid_{\mathrm{0},\mathrm{1}−{b}} ^{{a}−{b}+\mathrm{1}} \right) \\ $$
Commented by M±th+et£s last updated on 10/Apr/20

$${G}\:{is}\:{meijer}\:{function} \\ $$$${f}\:{is}\:{hypergeometric}\:{function} \\ $$
