Menu Close

elemeary-calculus-if-sin-3x-cos-3x-m-sin-x-cos-x-n-then-find-the-relatiomship-between-m-and-n-independent-of-x-

Tinku Tara 0 Comments
Pin




Question Number 127373 by mnjuly1970 last updated on 29/Dec/20
... elemeary calculus.. if { ((sin(3x)+cos(3x)=m)),((sin(x)+cos(x)=n)) :} then find the relatiomship between ′m′ and ′ n′ independent of ′ x′ ....
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{elemeary}\:\:\:{calculus}.. \\ $$$$\:\:{if}\:\:\:\:\begin{cases}{{sin}\left(\mathrm{3}{x}\right)+{cos}\left(\mathrm{3}{x}\right)={m}}\\{{sin}\left({x}\right)+{cos}\left({x}\right)={n}}\end{cases} \\ $$$$\:\:\:{then}\:\:\:{find}\:{the}\:{relatiomship} \\ $$$$\:\:\:{between}\:\:'{m}'\:{and}\:'\:{n}'\:{independent}\:{of} \\ $$$$\:\:'\:{x}'\:…. \\ $$
Answered by bemath last updated on 29/Dec/20
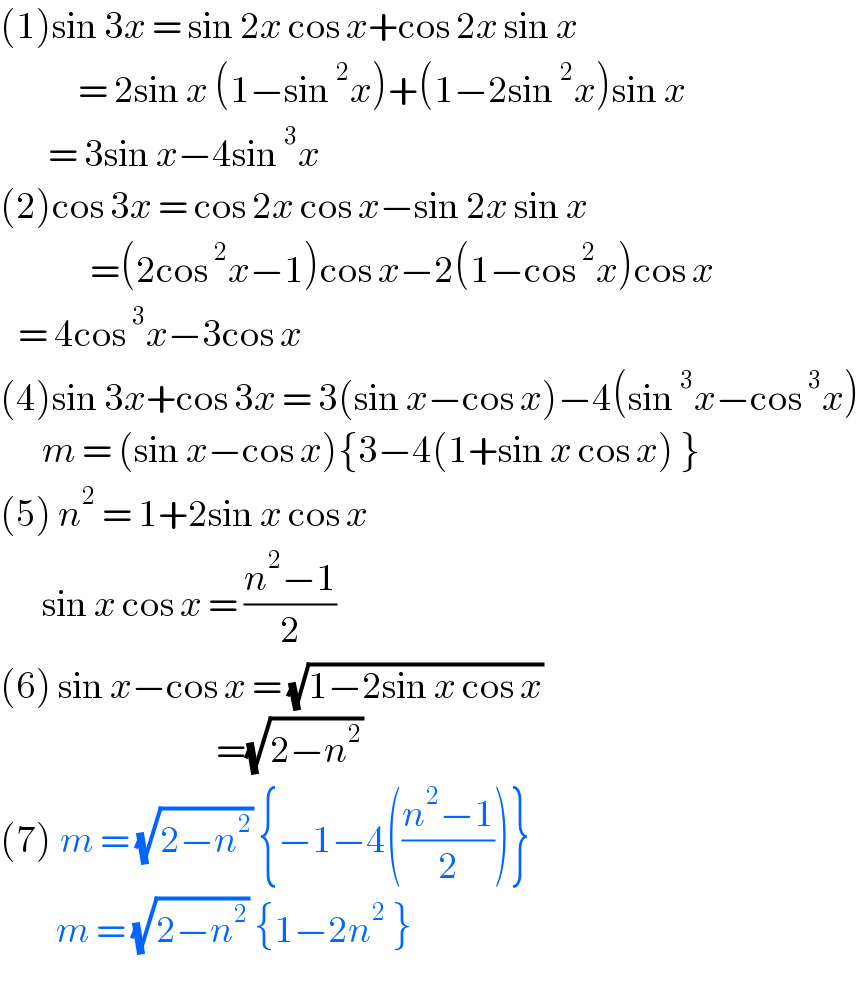
(1)sin 3x = sin 2x cos x+cos 2x sin x = 2sin x (1−sin^2 x)+(1−2sin^2 x)sin x = 3sin x−4sin^3 x (2)cos 3x = cos 2x cos x−sin 2x sin x =(2cos^2 x−1)cos x−2(1−cos^2 x)cos x = 4cos^3 x−3cos x (4)sin 3x+cos 3x = 3(sin x−cos x)−4(sin^3 x−cos^3 x) m = (sin x−cos x){3−4(1+sin x cos x) } (5) n^2 = 1+2sin x cos x sin x cos x = ((n^2 −1)/2) (6) sin x−cos x = (√(1−2sin x cos x)) =(√(2−n^2 )) (7) m = (√(2−n^2 )) {−1−4(((n^2 −1)/2))} m = (√(2−n^2 )) {1−2n^2 }
$$\left(\mathrm{1}\right)\mathrm{sin}\:\mathrm{3}{x}\:=\:\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{cos}\:{x}+\mathrm{cos}\:\mathrm{2}{x}\:\mathrm{sin}\:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2sin}\:{x}\:\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)+\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)\mathrm{sin}\:{x} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x} \\ $$$$\left(\mathrm{2}\right)\mathrm{cos}\:\mathrm{3}{x}\:=\:\mathrm{cos}\:\mathrm{2}{x}\:\mathrm{cos}\:{x}−\mathrm{sin}\:\mathrm{2}{x}\:\mathrm{sin}\:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}\right)\mathrm{cos}\:{x}−\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)\mathrm{cos}\:{x} \\ $$$$\:\:\:=\:\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x} \\ $$$$\left(\mathrm{4}\right)\mathrm{sin}\:\mathrm{3}{x}+\mathrm{cos}\:\mathrm{3}{x}\:=\:\mathrm{3}\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)−\mathrm{4}\left(\mathrm{sin}\:^{\mathrm{3}} {x}−\mathrm{cos}\:^{\mathrm{3}} {x}\right) \\ $$$$\:\:\:\:\:\:\:{m}\:=\:\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)\left\{\mathrm{3}−\mathrm{4}\left(\mathrm{1}+\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\right)\:\right\} \\ $$$$\left(\mathrm{5}\right)\:{n}^{\mathrm{2}} \:=\:\mathrm{1}+\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:=\:\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{6}\right)\:\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{1}−\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}−{n}^{\mathrm{2}} } \\ $$$$\left(\mathrm{7}\right)\:{m}\:=\:\sqrt{\mathrm{2}−{n}^{\mathrm{2}} }\:\left\{−\mathrm{1}−\mathrm{4}\left(\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:{m}\:=\:\sqrt{\mathrm{2}−{n}^{\mathrm{2}} }\:\left\{\mathrm{1}−\mathrm{2}{n}^{\mathrm{2}} \:\right\} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 29/Dec/20
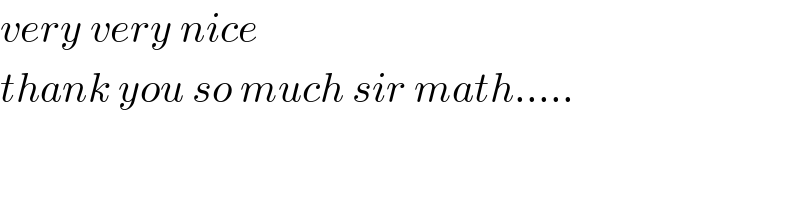
very very nice thank you so much sir math.....
$${very}\:{very}\:{nice}\: \\ $$$${thank}\:{you}\:{so}\:{much}\:{sir}\:{math}….. \\ $$
Commented by bemath last updated on 29/Dec/20
thank you master. christmas greetings from jerusalem
Commented by mnjuly1970 last updated on 29/Dec/20
god keep you merry christmas... peace be upon you...
$$\:{god}\:{keep}\:{you}\: \\ $$$${merry}\:\:{christmas}… \\ $$$${peace}\:{be}\:{upon}\:{you}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *