Question Number 120855 by mnjuly1970 last updated on 03/Nov/20
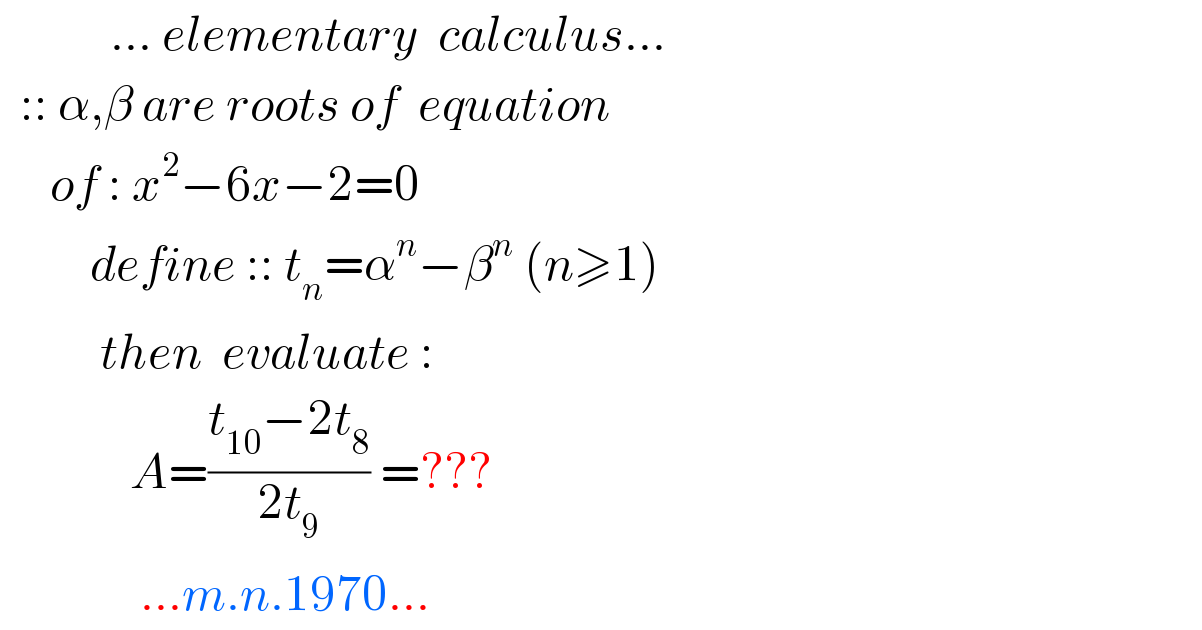
$$\:\:\:\:\:\:\:\:\:\:\:…\:{elementary}\:\:{calculus}… \\ $$$$\:\:::\:\alpha,\beta\:{are}\:{roots}\:{of}\:\:{equation} \\ $$$$\:\:\:\:\:{of}\::\:{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{define}\:::\:{t}_{{n}} =\alpha^{{n}} −\beta^{{n}} \:\left({n}\geqslant\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{then}\:\:{evaluate}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\frac{{t}_{\mathrm{10}} −\mathrm{2}{t}_{\mathrm{8}} }{\mathrm{2}{t}_{\mathrm{9}} }\:=??? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…{m}.{n}.\mathrm{1970}… \\ $$
Answered by TANMAY PANACEA last updated on 03/Nov/20
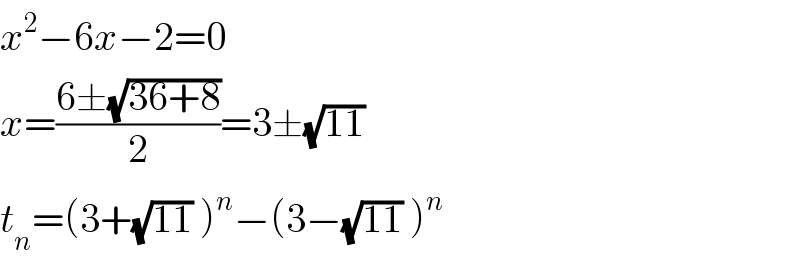
$${x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{2}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{6}\pm\sqrt{\mathrm{36}+\mathrm{8}}}{\mathrm{2}}=\mathrm{3}\pm\sqrt{\mathrm{11}}\: \\ $$$${t}_{{n}} =\left(\mathrm{3}+\sqrt{\mathrm{11}}\:\right)^{{n}} −\left(\mathrm{3}−\sqrt{\mathrm{11}}\:\right)^{{n}} \\ $$
Answered by mnjuly1970 last updated on 07/Nov/20
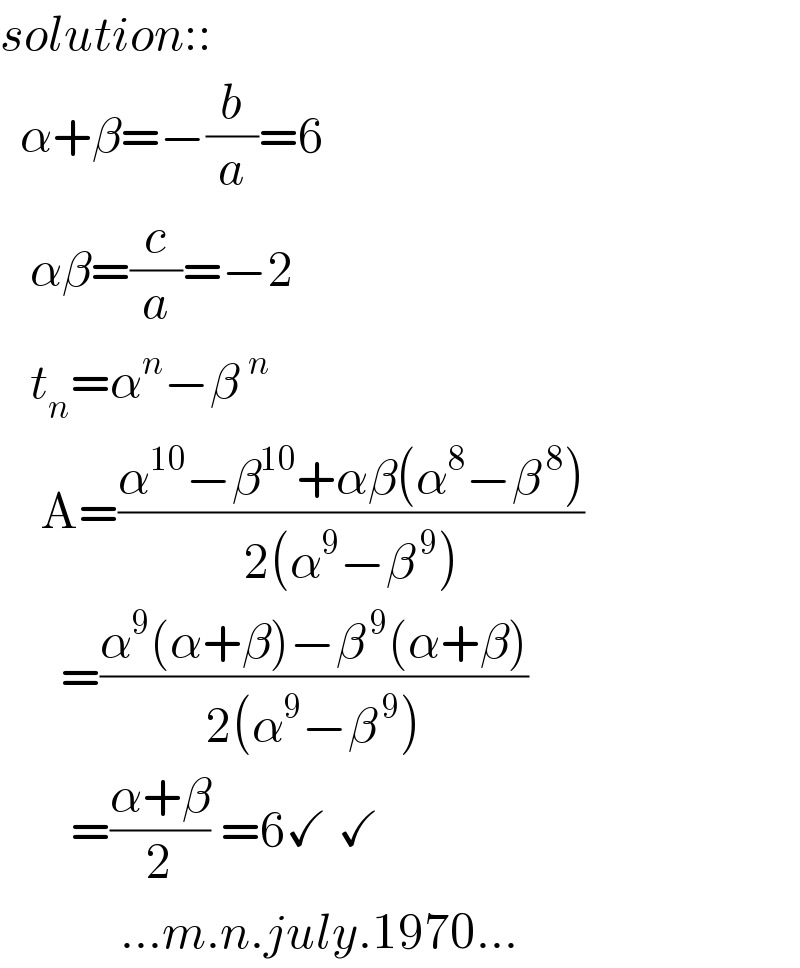
$${solution}:: \\ $$$$\:\:\alpha+\beta=−\frac{{b}}{{a}}=\mathrm{6} \\ $$$$\:\:\:\alpha\beta=\frac{{c}}{{a}}=−\mathrm{2} \\ $$$$\:\:\:{t}_{{n}} =\alpha^{{n}} −\beta\:^{{n}} \\ $$$$\:\:\:\:\mathrm{A}=\frac{\alpha^{\mathrm{10}} −\beta^{\mathrm{10}} +\alpha\beta\left(\alpha^{\mathrm{8}} −\beta^{\:\mathrm{8}} \right)}{\mathrm{2}\left(\alpha^{\mathrm{9}} −\beta^{\:\mathrm{9}} \right)} \\ $$$$\:\:\:\:\:\:=\frac{\alpha^{\mathrm{9}} \left(\alpha+\beta\right)−\beta^{\:\mathrm{9}} \left(\alpha+\beta\right)}{\mathrm{2}\left(\alpha^{\mathrm{9}} −\beta^{\:\mathrm{9}} \right)}\:\:\: \\ $$$$\:\:\:\:\:\:\:=\frac{\alpha+\beta}{\mathrm{2}}\:=\mathrm{6}\checkmark\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…{m}.{n}.{july}.\mathrm{1970}… \\ $$
