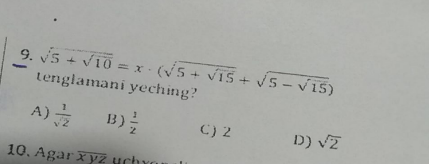Question Number 109222 by bemath last updated on 22/Aug/20
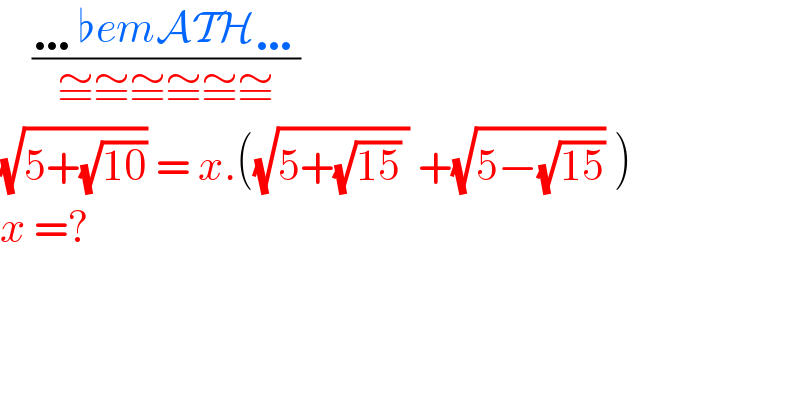
$$\:\:\:\:\frac{\ldots\flat{em}\mathcal{ATH}\ldots}{\cong\cong\cong\cong\cong\cong} \\ $$$$\sqrt{\mathrm{5}+\sqrt{\mathrm{10}}}\:=\:{x}.\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{15}}\:}\:+\sqrt{\mathrm{5}−\sqrt{\mathrm{15}}}\:\right) \\ $$$${x}\:=? \\ $$
Answered by bobhans last updated on 22/Aug/20
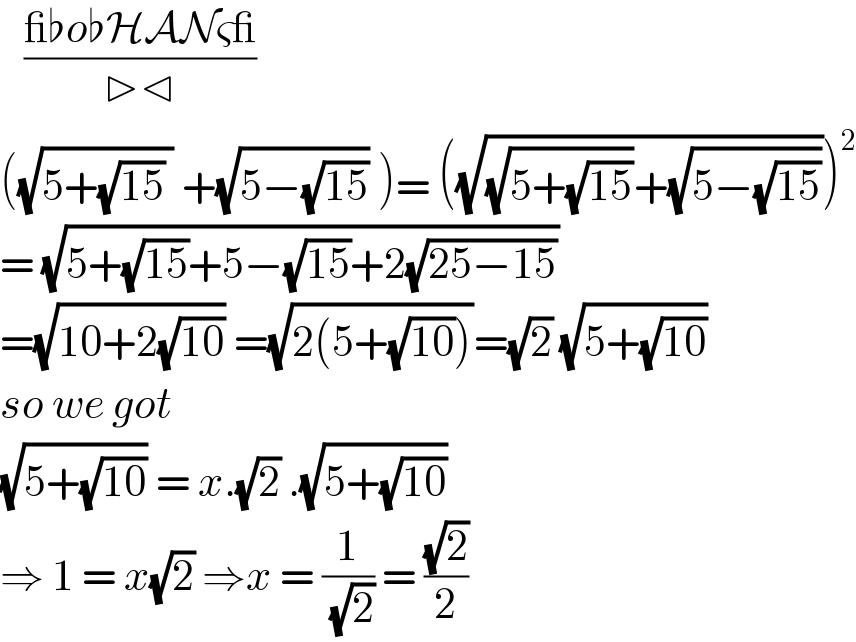
$$\:\:\:\frac{\_\flat{o}\flat\mathcal{HAN}\varsigma\_}{\triangleright\triangleleft} \\ $$$$\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{15}}\:}\:+\sqrt{\mathrm{5}−\sqrt{\mathrm{15}}}\:\right)=\:\left(\sqrt{\sqrt{\mathrm{5}+\sqrt{\mathrm{15}}}+\sqrt{\mathrm{5}−\sqrt{\mathrm{15}}}}\right)^{\mathrm{2}} \\ $$$$=\:\sqrt{\mathrm{5}+\sqrt{\mathrm{15}}+\mathrm{5}−\sqrt{\mathrm{15}}+\mathrm{2}\sqrt{\mathrm{25}−\mathrm{15}}} \\ $$$$=\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{10}}}\:=\sqrt{\mathrm{2}\left(\mathrm{5}+\sqrt{\mathrm{10}}\right)}=\sqrt{\mathrm{2}}\:\sqrt{\mathrm{5}+\sqrt{\mathrm{10}}} \\ $$$${so}\:{we}\:{got}\: \\ $$$$\sqrt{\mathrm{5}+\sqrt{\mathrm{10}}}\:=\:{x}.\sqrt{\mathrm{2}}\:.\sqrt{\mathrm{5}+\sqrt{\mathrm{10}}} \\ $$$$\Rightarrow\:\mathrm{1}\:=\:{x}\sqrt{\mathrm{2}}\:\Rightarrow{x}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 22/Aug/20

$${yes}…{thank}\:{you} \\ $$
Commented by bemath last updated on 22/Aug/20