Question Number 109091 by bemath last updated on 21/Aug/20
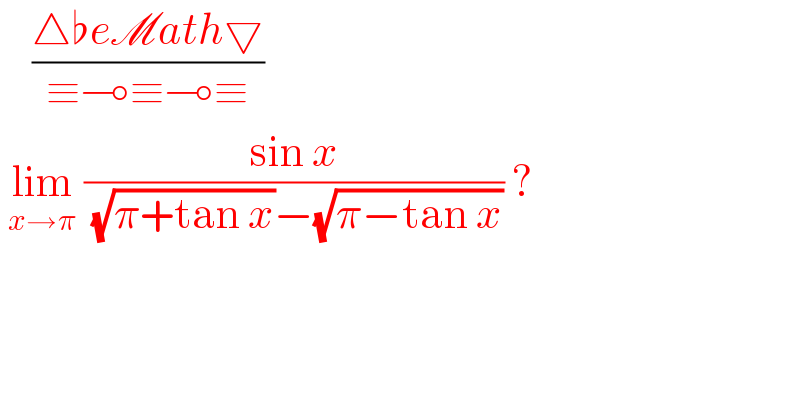
$$\:\:\:\:\frac{\bigtriangleup\flat{e}\mathscr{M}{ath}\bigtriangledown}{\equiv\multimap\equiv\multimap\equiv} \\ $$$$\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}}{\:\sqrt{\pi+\mathrm{tan}\:{x}}−\sqrt{\pi−\mathrm{tan}\:{x}}}\:? \\ $$
Answered by bobhans last updated on 21/Aug/20

Commented by bobhans last updated on 21/Aug/20
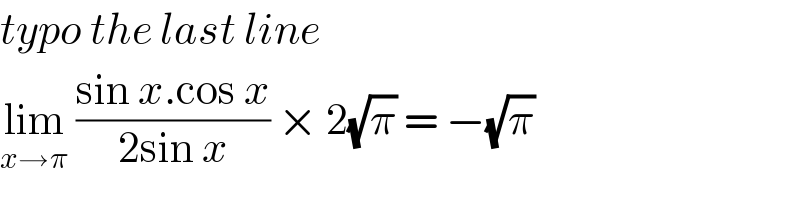
$${typo}\:{the}\:{last}\:{line}\: \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}.\mathrm{cos}\:{x}}{\mathrm{2sin}\:{x}}\:×\:\mathrm{2}\sqrt{\pi}\:=\:−\sqrt{\pi}\: \\ $$
Answered by bemath last updated on 21/Aug/20
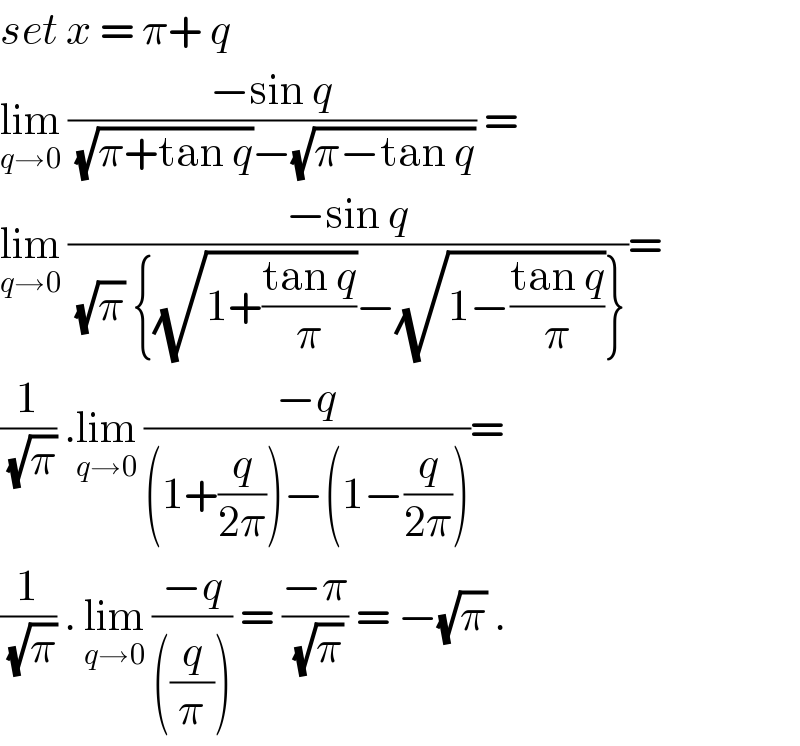
$${set}\:{x}\:=\:\pi+\:{q}\: \\ $$$$\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:{q}}{\:\sqrt{\pi+\mathrm{tan}\:{q}}−\sqrt{\pi−\mathrm{tan}\:{q}}}\:=\: \\ $$$$\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:{q}}{\:\sqrt{\pi}\:\left\{\sqrt{\mathrm{1}+\frac{\mathrm{tan}\:{q}}{\pi}}−\sqrt{\mathrm{1}−\frac{\mathrm{tan}\:{q}}{\pi}}\right\}}= \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\pi}}\:.\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{q}}{\left(\mathrm{1}+\frac{{q}}{\mathrm{2}\pi}\right)−\left(\mathrm{1}−\frac{{q}}{\mathrm{2}\pi}\right)}= \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\pi}}\:.\:\underset{{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{q}}{\left(\frac{{q}}{\pi}\right)}\:=\:\frac{−\pi}{\:\sqrt{\pi}}\:=\:−\sqrt{\pi}\:. \\ $$
