Question Number 164609 by SANOGO last updated on 19/Jan/22
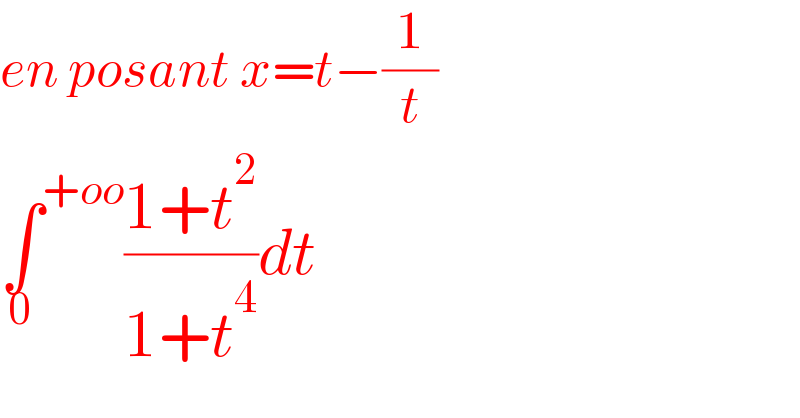
$${en}\:{posant}\:{x}={t}−\frac{\mathrm{1}}{{t}} \\ $$$$\underset{\mathrm{0}} {\int}^{+{oo}} \frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }{dt} \\ $$
Answered by Mathspace last updated on 19/Jan/22
![I=∫_0 ^∞ ((1+(1/t^2 ))/(t^2 +(1/t^2 ))) dt =∫_0 ^∞ ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt =_(t−(1/t)=x) ∫_(−∞) ^(+∞ ) (dx/(x^2 +2)) =_(x=(√2)y) ∫_(−∞) ^(+∞ ) (((√2)dy)/(2(1+y^2 ))) =((√2)/2)[arctan(y)]_(−∞) ^(+∞) =((√2)/2)((π/2)+(π/2))=((π(√2))/2)](https://www.tinkutara.com/question/Q164610.png)
$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\:{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}}{dt} \\ $$$$=_{{t}−\frac{\mathrm{1}}{{t}}={x}} \:\int_{−\infty} ^{+\infty\:} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}} \\ $$$$=_{{x}=\sqrt{\mathrm{2}}{y}} \:\:\int_{−\infty} ^{+\infty\:} \frac{\sqrt{\mathrm{2}}{dy}}{\mathrm{2}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left[{arctan}\left({y}\right)\right]_{−\infty} ^{+\infty} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by SANOGO last updated on 19/Jan/22
$${merci}\:{bien}\: \\ $$
