Entry-to-a-certain-University-is-determined-by-a-national-test-The-scores-on-this-test-are-normally-distributed-with-a-mean-of-500-and-a-standard-deviation-of-100-a-Find-the-probability-that-a

Question Number 169802 by MathsFan last updated on 09/May/22

$$$$Entry to a certain University is determined by a national test. The scores on this test are normally
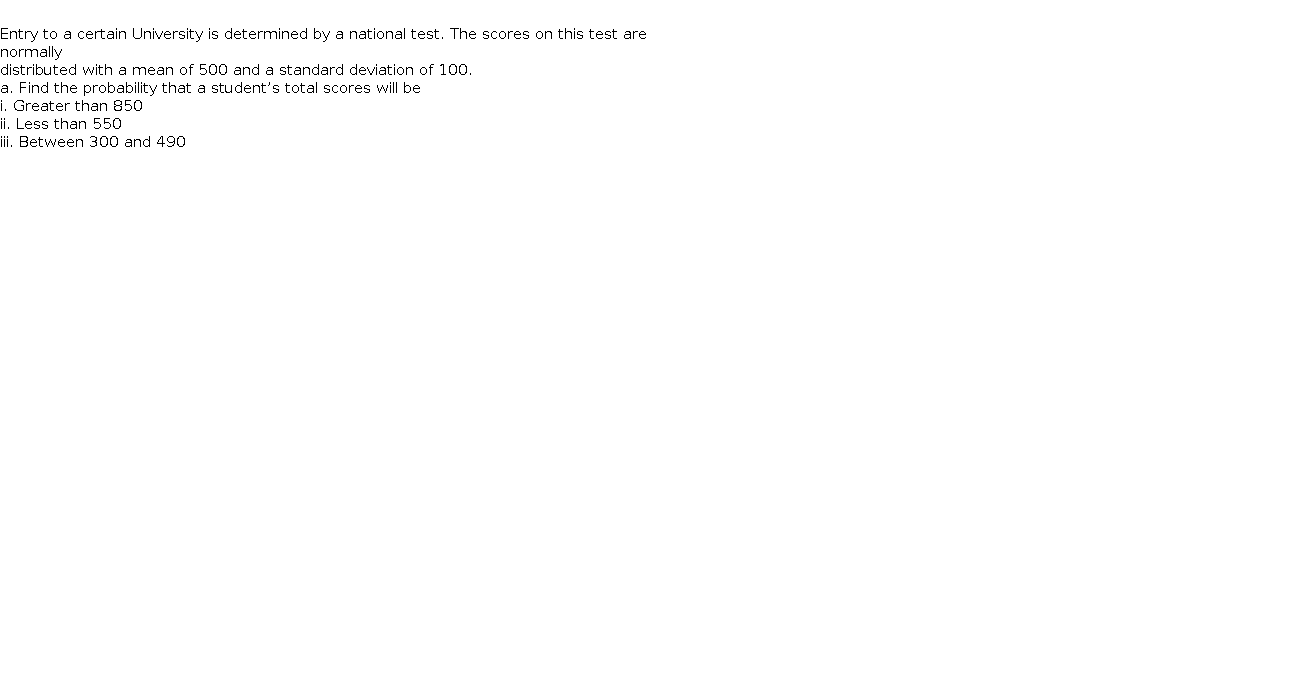
distributed with a mean of 500 and a standard deviation of 100.
a. Find the probability that a student’s total scores will be
i. Greater than 850
ii. Less than 550
iii. Between 300 and 490

Answered by shikaridwan last updated on 10/May/22

$$f\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\left(\frac{x-\mu }{\sigma }\right)}^2}{2}}$$$$here\sigma =100\mu =500$$$$P(X>850)=\frac{1}{100\sqrt{2\pi }}{\int }_{850}^{\mathrm{\infty }}exp(-\frac{{\left(\frac{x-500}{100}\right)}^2}{2})dx$$$$=\frac{1}{\sqrt{2\pi }}{\int }_{3.5}^{\mathrm{\infty }}exp(-t^2/2)dtt=\frac{x-500}{100}$$$$=\frac{1}{\sqrt{2\pi }}{\int }_0^{\mathrm{\infty }}exp(-t^2/2)dt-\frac{1}{\sqrt{2\pi }}{\int }_0^{3.5}{e}^{-t^2/2}dt$$$$=\frac{1}{2}-\frac{1}{\sqrt{\pi }}{\int }_0^{\sqrt{2}\times 3.5}{e}^{-u^2}du$$$$=\frac{1}{2}(1-erf(\sqrt{2}\times 3.5))$$$$P(X<550)={\int }_{-\mathrm{\infty }}^{550}f\left(x\right)dx$$$$P(300<X<490)={\int }_{300}^{490}f\left(x\right)dx$$

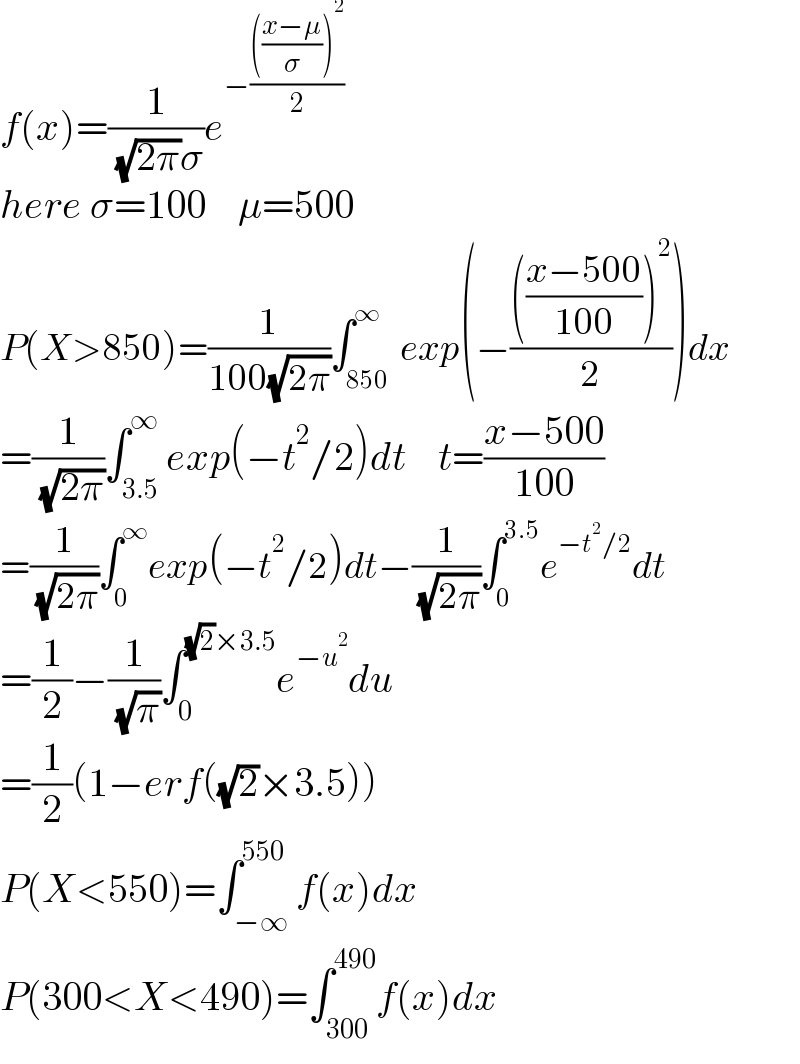
Commented by MathsFan last updated on 10/May/22

$$wow$$$$thankyousir$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com