Question Number 144186 by cherokeesay last updated on 22/Jun/21
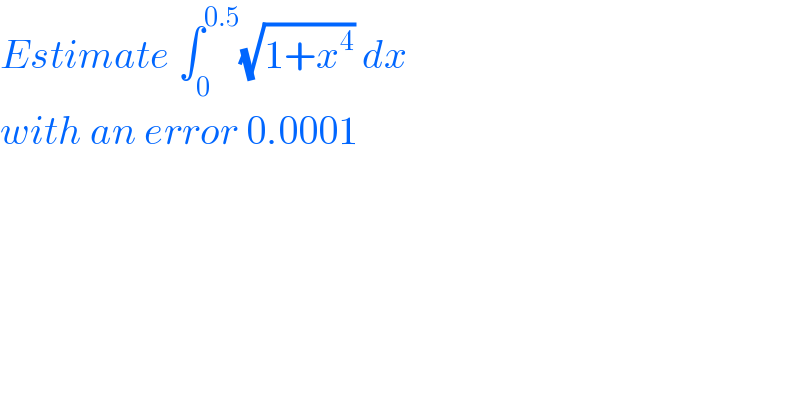
$${Estimate}\:\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{5}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx} \\ $$$${with}\:{an}\:{error}\:\mathrm{0}.\mathrm{0001} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jun/21
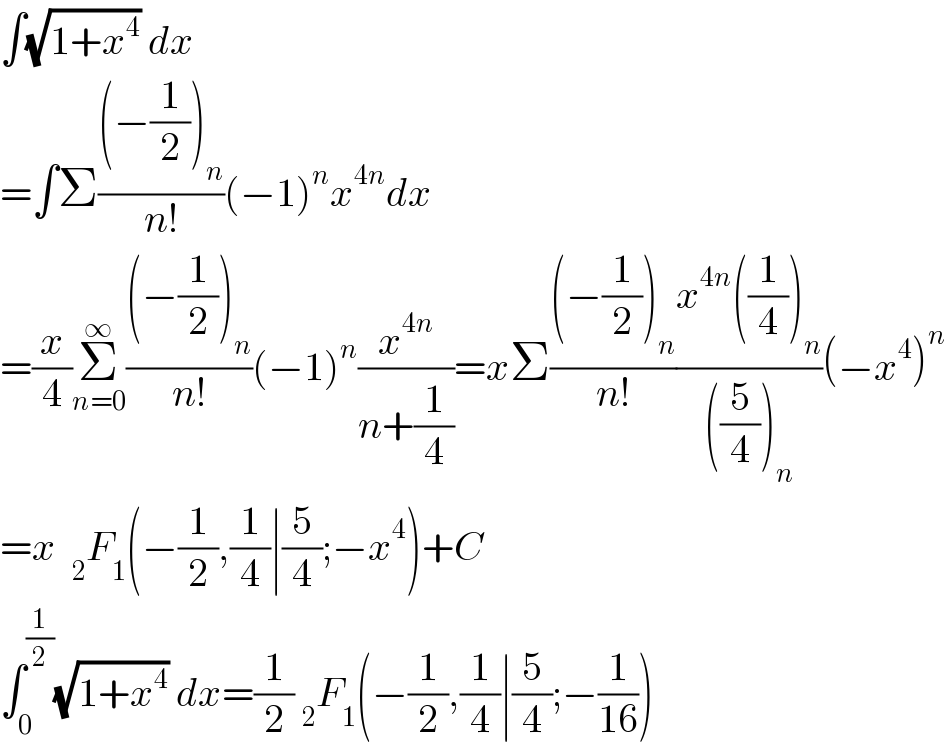
$$\int\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx} \\ $$$$=\int\Sigma\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{4}{n}} {dx} \\ $$$$=\frac{{x}}{\mathrm{4}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}} }{{n}+\frac{\mathrm{1}}{\mathrm{4}}}={x}\Sigma\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\frac{{x}^{\mathrm{4}{n}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)_{{n}} }{\left(\frac{\mathrm{5}}{\mathrm{4}}\right)_{{n}} }\left(−{x}^{\mathrm{4}} \right)^{{n}} \\ $$$$={x}\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}}\mid\frac{\mathrm{5}}{\mathrm{4}};−{x}^{\mathrm{4}} \right)+{C} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{4}}\mid\frac{\mathrm{5}}{\mathrm{4}};−\frac{\mathrm{1}}{\mathrm{16}}\right) \\ $$
Commented by cherokeesay last updated on 23/Jun/21

$${thank}\:{you}\:{sir}. \\ $$
Answered by mathmax by abdo last updated on 23/Jun/21
![we have (1+x)^α =1+αx +((α(α−1))/2)x^2 +.... ⇒ (1+x)^(1/2) =1+(x/2) −(1/8)x^2 +... ⇒1+(x/2)−(x^2 /8)≤(√(1+x))≤1+(x/2) we change x by x^4 ⇒1+(x^4 /2)−(x^8 /8)≤(√(1+x^4 ))≤1+(x^4 /2) ⇒ ∫_0 ^(1/2) (1+(x^4 /2)−(x^8 /8))dx≤∫_0 ^(1/2) (√(1+x^4 ))dx≤∫_0 ^(1/2) (1+(x^4 /2))dx we have ∫_0 ^(1/2) (1+(x^4 /2)−(x^8 /8))dx=[x+(1/(10))x^5 −(1/(72))x^9 ]_0 ^(1/2) =(1/2)+(1/(10.2^5 ))−(1/(72.2^9 )) ∫_0 ^(1/2) (1+(x^4 /2))x=[x+(1/(10))x^5 ]_0 ^(1/2) =(1/2)+(1/(10.2^5 )) ⇒ (1/2)+(1/(10.2^5 ))−(1/(72.2^9 ))≤∫_0 ^(1/2) (√(1+x^4 ))dx≤(1/2)+(1/(10.2^5 )) the best value of this integral is v_0 =(1/4)+(1/(10.2^6 ))−(1/(72.2^(10) ))+(1/4)+(1/(10.2^6 )) =(1/2)+(1/(5.2^6 ))−(1/(72.2^(10) ))](https://www.tinkutara.com/question/Q144229.png)
$$\mathrm{we}\:\mathrm{have}\:\left(\mathrm{1}+\mathrm{x}\right)^{\alpha} \:=\mathrm{1}+\alpha\mathrm{x}\:+\frac{\alpha\left(\alpha−\mathrm{1}\right)}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:+….\:\Rightarrow \\ $$$$\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{1}+\frac{\mathrm{x}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} +…\:\Rightarrow\mathrm{1}+\frac{\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{8}}\leqslant\sqrt{\mathrm{1}+\mathrm{x}}\leqslant\mathrm{1}+\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{change}\:\mathrm{x}\:\mathrm{by}\:\mathrm{x}^{\mathrm{4}} \:\Rightarrow\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{8}}\leqslant\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\leqslant\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{8}}\right)\mathrm{dx}\leqslant\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\leqslant\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}\right)\mathrm{dx}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{8}}\right)\mathrm{dx}=\left[\mathrm{x}+\frac{\mathrm{1}}{\mathrm{10}}\mathrm{x}^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{72}}\mathrm{x}^{\mathrm{9}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{10}.\mathrm{2}^{\mathrm{5}} }−\frac{\mathrm{1}}{\mathrm{72}.\mathrm{2}^{\mathrm{9}} } \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}}\right)\mathrm{x}=\left[\mathrm{x}+\frac{\mathrm{1}}{\mathrm{10}}\mathrm{x}^{\mathrm{5}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{10}.\mathrm{2}^{\mathrm{5}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{10}.\mathrm{2}^{\mathrm{5}} }−\frac{\mathrm{1}}{\mathrm{72}.\mathrm{2}^{\mathrm{9}} }\leqslant\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\leqslant\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{10}.\mathrm{2}^{\mathrm{5}} } \\ $$$$\mathrm{the}\:\mathrm{best}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is} \\ $$$$\mathrm{v}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{10}.\mathrm{2}^{\mathrm{6}} }−\frac{\mathrm{1}}{\mathrm{72}.\mathrm{2}^{\mathrm{10}} }+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{10}.\mathrm{2}^{\mathrm{6}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{5}.\mathrm{2}^{\mathrm{6}} }−\frac{\mathrm{1}}{\mathrm{72}.\mathrm{2}^{\mathrm{10}} } \\ $$
