Question Number 151197 by KONE last updated on 18/Aug/21
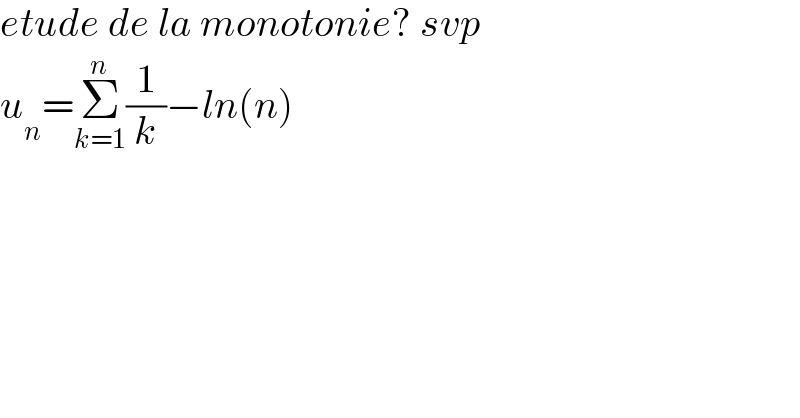
$${etude}\:{de}\:{la}\:{monotonie}?\:{svp} \\ $$$${u}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}−{ln}\left({n}\right) \\ $$
Answered by mathmax by abdo last updated on 19/Aug/21
![f(x)=logx ∃c ∈]n,n+1[ /log(n+1)−logn=(1/c) n<c<n+1 ⇒(1/(n+1))<(1/c)<(1/n) ⇒Σ_(k=1) ^n (1/(k+1))<Σ_(k=1) ^n log(k+1)−logk<Σ_(k=1) ^n (1/k) ⇒Σ_(k=2) ^(n+1) (1/k)<log(n+1)<H_n ⇒H_n −1+(1/(n+1))<log(n+1)<H_n ⇒(1/(n+1))−1<log(n+1)−H_n <0 ⇒0<H_n −log(n+1)<1−(1/(n+1)) ⇒0<H_n −log(n)−log(1+(1/n))<(n/(n+1)) ⇒ log(1+(1/n))<H_n −logn<(n/(n+1))−log(1+(1/n)) on passe a la limite on obtient o≤lim(H_n −logn)≤1 rest de montere que u_n est monotone? u_(n+1) −u_n =Σ_(k=1) ^(n+1) (1/k)−ln(n+1)−Σ_(k=1) ^n (1/k)+ln(n) =(1/(n+1))+ln((n/(n+1)))=(1/(n+1))+ln(1−(1/(n+1))) let Φ(x)=(1/x)+ln(1−(1/x)) x>1 lim_(x→1^+ ) Φ(x)=−∞ lim_(x→+∞) =0 et Φ^′ (x)=−(1/x^2 )+(1/(x^2 (1−(1/x)))) =(1/x^2 )((1/(1−(1/x)))−1)=(1/x^2 )((x/(x−1))−1) =(1/x^2 )((1/(x−1)))>0 ⇒Φ(x)<0 sur]1,+∞[ ⇒u_(n+1) −u_n <0 ⇒u_n )est decroissante lim_(n→+∞) =γ et on prouve que 0≤γ≤1](https://www.tinkutara.com/question/Q151201.png)
$$\left.\mathrm{f}\left(\mathrm{x}\right)=\mathrm{logx}\:\:\:\:\:\:\exists\mathrm{c}\:\in\right]\mathrm{n},\mathrm{n}+\mathrm{1}\left[\:\:/\mathrm{log}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{logn}=\frac{\mathrm{1}}{\mathrm{c}}\right. \\ $$$$\mathrm{n}<\mathrm{c}<\mathrm{n}+\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}<\frac{\mathrm{1}}{\mathrm{c}}<\frac{\mathrm{1}}{\mathrm{n}}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}<\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{log}\left(\mathrm{k}+\mathrm{1}\right)−\mathrm{logk}<\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}} \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}}<\mathrm{log}\left(\mathrm{n}+\mathrm{1}\right)<\mathrm{H}_{\mathrm{n}} \:\Rightarrow\mathrm{H}_{\mathrm{n}} −\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}<\mathrm{log}\left(\mathrm{n}+\mathrm{1}\right)<\mathrm{H}_{\mathrm{n}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\mathrm{1}<\mathrm{log}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{H}_{\mathrm{n}} <\mathrm{0}\:\Rightarrow\mathrm{0}<\mathrm{H}_{\mathrm{n}} −\mathrm{log}\left(\mathrm{n}+\mathrm{1}\right)<\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{0}<\mathrm{H}_{\mathrm{n}} −\mathrm{log}\left(\mathrm{n}\right)−\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)<\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)<\mathrm{H}_{\mathrm{n}} −\mathrm{logn}<\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}−\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\:\:\mathrm{on}\:\mathrm{passe}\:\mathrm{a}\:\mathrm{la}\:\mathrm{limite} \\ $$$$\mathrm{on}\:\mathrm{obtient}\:\:\mathrm{o}\leqslant\mathrm{lim}\left(\mathrm{H}_{\mathrm{n}} −\mathrm{logn}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{rest}\:\mathrm{de}\:\mathrm{montere}\:\mathrm{que}\:\mathrm{u}_{\mathrm{n}} \:\mathrm{est}\:\mathrm{monotone}? \\ $$$$\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{u}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}}−\mathrm{ln}\left(\mathrm{n}+\mathrm{1}\right)−\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}+\mathrm{ln}\left(\mathrm{n}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\mathrm{ln}\left(\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right) \\ $$$$\mathrm{let}\:\Phi\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)\:\:\:\mathrm{x}>\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\Phi\left(\mathrm{x}\right)=−\infty \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} =\mathrm{0}\:\:\:\:\:\:\mathrm{et}\:\Phi^{'} \left(\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}−\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)>\mathrm{0} \\ $$$$\left.\Rightarrow\Phi\left(\mathrm{x}\right)<\mathrm{0}\:\mathrm{sur}\right]\mathrm{1},+\infty\left[\:\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\mathrm{u}_{\mathrm{n}} <\mathrm{0}\:\Rightarrow\mathrm{u}_{\mathrm{n}} \right)\mathrm{est}\:\mathrm{decroissante} \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} =\gamma\:\:\mathrm{et}\:\mathrm{on}\:\mathrm{prouve}\:\mathrm{que}\:\mathrm{0}\leqslant\gamma\leqslant\mathrm{1} \\ $$
