Question Number 167782 by SANOGO last updated on 24/Mar/22
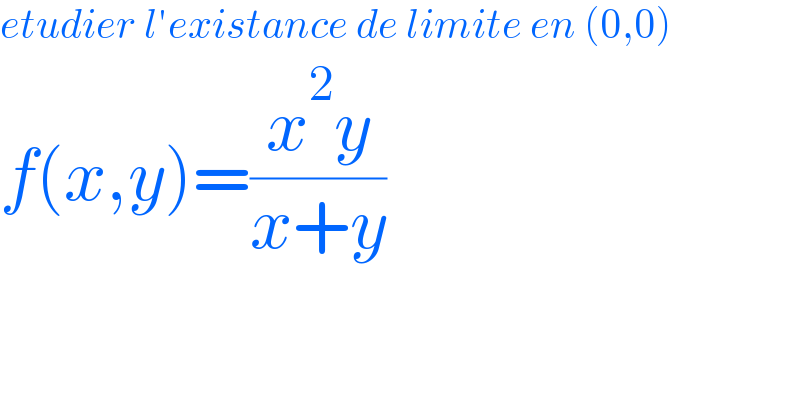
$${etudier}\:{l}'{existance}\:{de}\:{limite}\:{en}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${f}\left({x},{y}\right)=\frac{{x}^{\mathrm{2}} {y}}{{x}+{y}} \\ $$
Answered by Mathspace last updated on 25/Mar/22
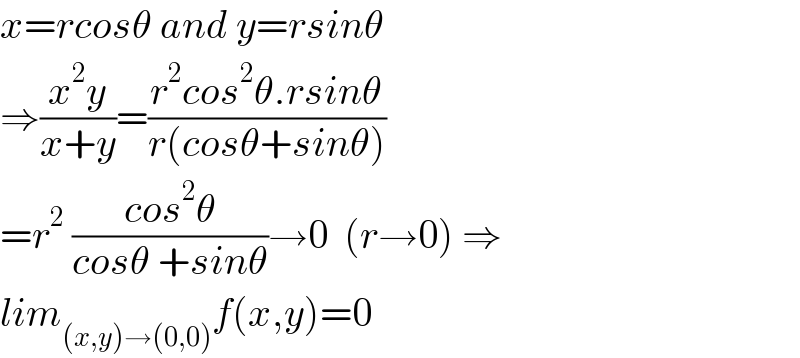
$${x}={rcos}\theta\:{and}\:{y}={rsin}\theta \\ $$$$\Rightarrow\frac{{x}^{\mathrm{2}} {y}}{{x}+{y}}=\frac{{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta.{rsin}\theta}{{r}\left({cos}\theta+{sin}\theta\right)} \\ $$$$={r}^{\mathrm{2}} \:\frac{{cos}^{\mathrm{2}} \theta}{{cos}\theta\:+{sin}\theta}\rightarrow\mathrm{0}\:\:\left({r}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$${lim}_{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {f}\left({x},{y}\right)=\mathrm{0} \\ $$
Commented by SANOGO last updated on 25/Mar/22
$${merci} \\ $$
