Question Number 154337 by SANOGO last updated on 17/Sep/21
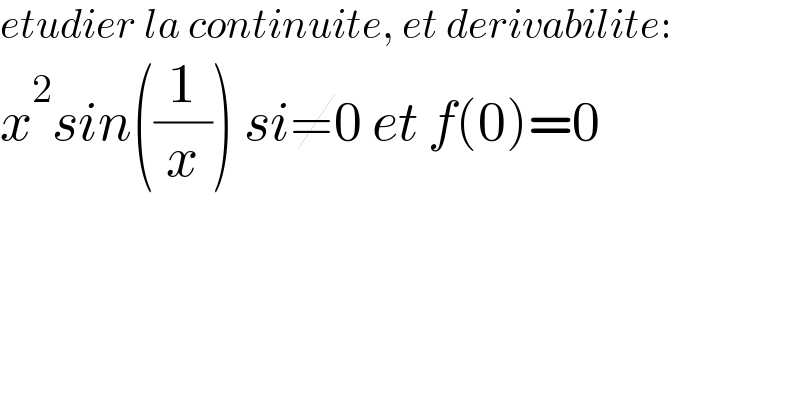
$${etudier}\:{la}\:{continuite},\:{et}\:{derivabilite}: \\ $$$${x}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{{x}}\right)\:{si}\neq\mathrm{0}\:{et}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Answered by puissant last updated on 17/Sep/21

$${posons}:\begin{cases}{{f}\left(\mathrm{0}\right)=\mathrm{0}\:{si}\:{x}=\mathrm{0}\:}\\{{f}\left({x}\right)={x}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{{x}}\right)\:,\:{sinon}..}\end{cases} \\ $$$$\ast\:{Continuit}\acute {{e}}\::\: \\ $$$$ \\ $$$${Premiere}\:{methode}: \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}{f}\left({x}\right)=\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}{f}\left({x}\right)=\mathrm{0}\:{et}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${alors},\:{f}\left({x}\right)\:{est}\:{continu}\:{sur}\:\mathbb{R}.. \\ $$$$ \\ $$$${Deuxieme}\:{methode}: \\ $$$$ \\ $$$${les}\:{fonctons}\:{carr}\acute {{e}}\left({x}^{\mathrm{2}} \right),\:{sin}\:{et}\:{inverse}\:\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${sont}\:{continus}\:{sur}\:\mathbb{R}\:{donc}\:{leur}\:{compos}\acute {{e}} \\ $$$${f}\left({x}\right)\:{est}\:{continu}\:{sur}\:\mathbb{R}.. \\ $$$$ \\ $$$$\ast\:{Derivabilit}\acute {{e}}\::\: \\ $$$$ \\ $$$${on}\:{a}\::\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}\right)−{f}\left(\mathrm{0}\right)}{{x}−\mathrm{0}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{xsin}\left(\frac{\mathrm{1}}{{x}}\right).. \\ $$$${on}\:{a}:\:\:−\mathrm{1}\leqslant{sin}\left(\frac{\mathrm{1}}{{x}}\right)\leqslant\mathrm{1}\:\rightarrow−{x}\leqslant{xsin}\left(\frac{\mathrm{1}}{{x}}\right)\leqslant{x} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{xsin}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}\:{d}'{apres}\:{le}\:{theoreme} \\ $$$${des}\:{gendarmes}.. \\ $$$${D}'{ou}\:{f}\:{est}\:{derivable}\:{sur}\:\mathbb{R}^{\ast} ..\: \\ $$
Commented by SANOGO last updated on 17/Sep/21
$${le}\:{puissant}\:{a}\:{parler}\:{merci}\:{bien} \\ $$
Commented by puissant last updated on 17/Sep/21

$${De}\:{rien}\:.. \\ $$
Answered by Jonathanwaweh last updated on 17/Sep/21
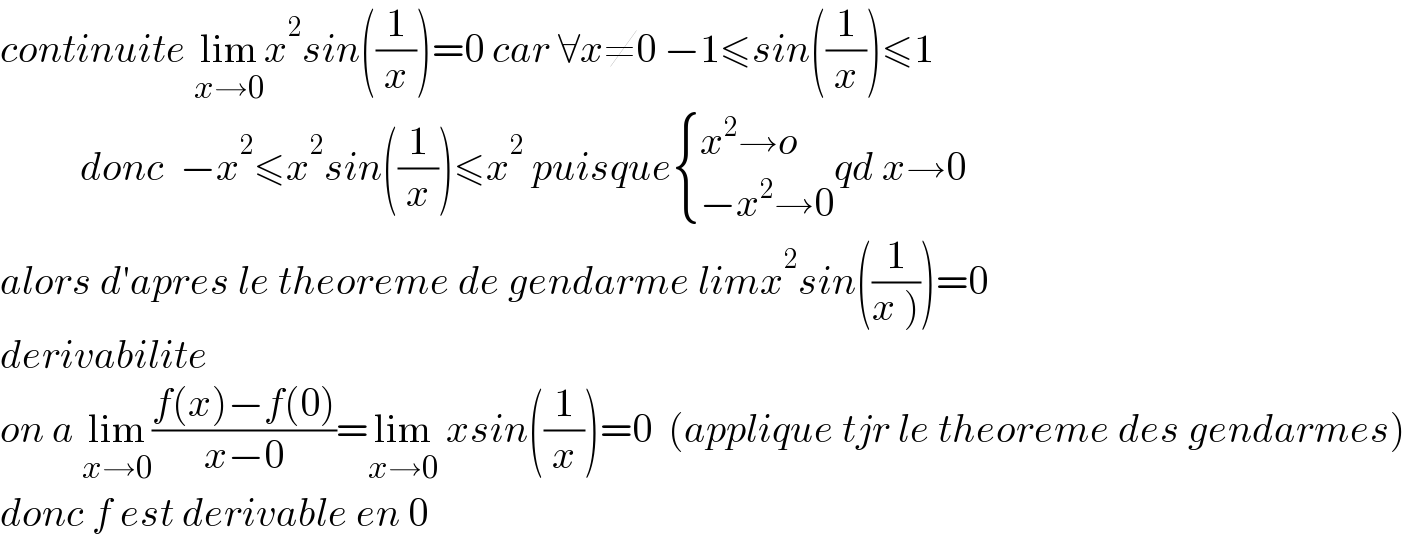
$${continuite}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}\:{car}\:\forall{x}\neq\mathrm{0}\:−\mathrm{1}\leqslant{sin}\left(\frac{\mathrm{1}}{{x}}\right)\leqslant\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:{donc}\:\:−{x}^{\mathrm{2}} \leqslant{x}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{{x}}\right)\leqslant{x}^{\mathrm{2}} \:{puisque\begin{cases}{{x}^{\mathrm{2}} \rightarrow{o}}\\{−{x}^{\mathrm{2}} \rightarrow\mathrm{0}}\end{cases}qd}\:{x}\rightarrow\mathrm{0} \\ $$$${alors}\:{d}'{apres}\:{le}\:{theoreme}\:{de}\:{gendarme}\:{limx}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{\left.{x}\:\right)}\right)=\mathrm{0} \\ $$$${derivabilite}\: \\ $$$${on}\:{a}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{f}\left({x}\right)−{f}\left(\mathrm{0}\right)}{{x}−\mathrm{0}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{xsin}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}\:\:\left({applique}\:{tjr}\:{le}\:{theoreme}\:{des}\:{gendarmes}\right) \\ $$$${donc}\:{f}\:{est}\:{derivable}\:{en}\:\mathrm{0} \\ $$
Commented by SANOGO last updated on 17/Sep/21
$${merci}\:{bien} \\ $$
Commented by puissant last updated on 17/Sep/21
$${Bien}\:{Mr}\:{jonathan}.. \\ $$
