Question Number 161020 by SANOGO last updated on 10/Dec/21
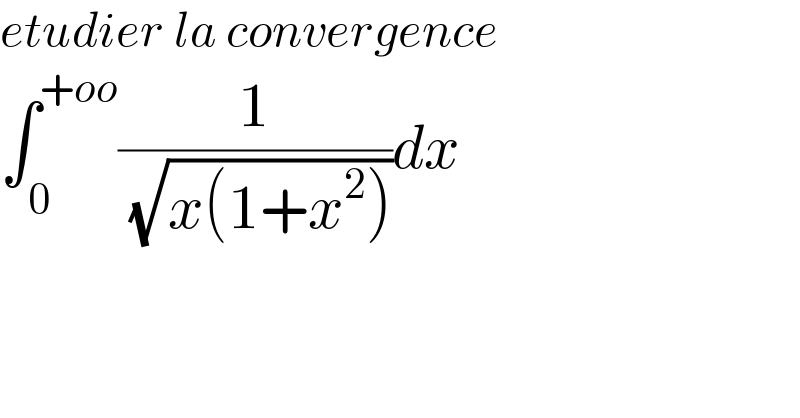
$${etudier}\:{la}\:{convergence} \\ $$$$\int_{\mathrm{0}} ^{+{oo}} \frac{\mathrm{1}}{\:\sqrt{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}}{dx} \\ $$
Answered by Ar Brandon last updated on 10/Dec/21
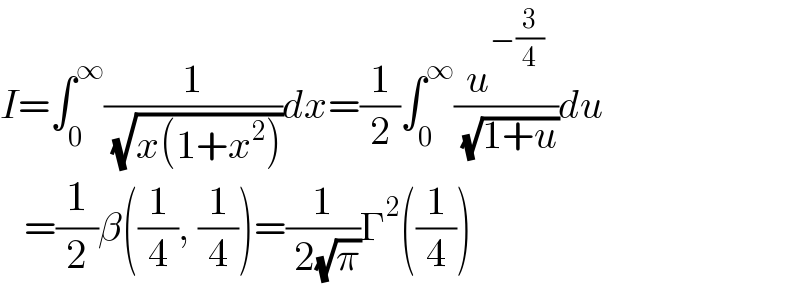
$${I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\:\sqrt{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{3}}{\mathrm{4}}} }{\:\sqrt{\mathrm{1}+{u}}}{du} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{1}}{\mathrm{4}},\:\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\pi}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$
Commented by SANOGO last updated on 11/Dec/21
$${merci}\:{bien} \\ $$
