Question Number 97683 by Don08q last updated on 09/Jun/20
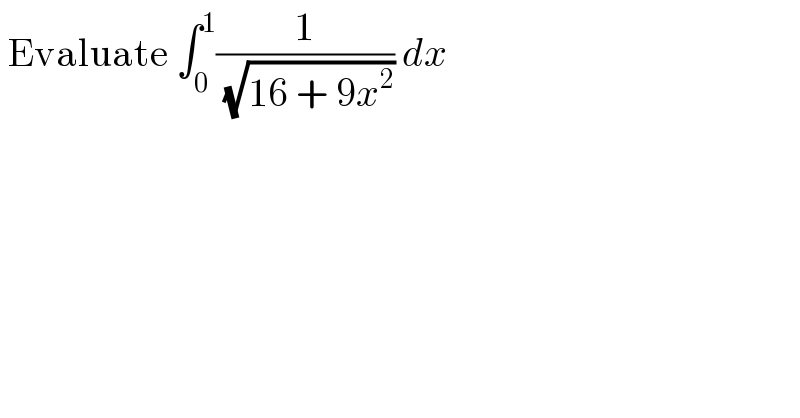
$$\:\mathrm{Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{16}\:+\:\mathrm{9}{x}^{\mathrm{2}} }}\:{dx} \\ $$
Commented by bemath last updated on 09/Jun/20
![set 3x = 4tan z ⇒3dx=4sec^2 zdz I=∫ (((4/3)sec^2 z dz)/( (√(16+16tan^2 z)))) I= (1/3)∫ sec z dz = (1/3) ln∣sec z+tan z∣ I= (1/3)[ln∣((√(16+9x^2 ))/4)+((3x)/4)∣]_0 ^1 =(1/3)ln(2)](https://www.tinkutara.com/question/Q97689.png)
$$\mathrm{set}\:\mathrm{3x}\:=\:\mathrm{4tan}\:\mathrm{z}\:\Rightarrow\mathrm{3dx}=\mathrm{4sec}\:^{\mathrm{2}} \mathrm{zdz} \\ $$$$\mathrm{I}=\int\:\frac{\frac{\mathrm{4}}{\mathrm{3}}\mathrm{sec}\:^{\mathrm{2}} \mathrm{z}\:\mathrm{dz}}{\:\sqrt{\mathrm{16}+\mathrm{16tan}\:^{\mathrm{2}} \mathrm{z}}} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\mathrm{sec}\:\mathrm{z}\:\mathrm{dz}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{ln}\mid\mathrm{sec}\:\mathrm{z}+\mathrm{tan}\:\mathrm{z}\mid\: \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{ln}\mid\frac{\sqrt{\mathrm{16}+\mathrm{9x}^{\mathrm{2}} }}{\mathrm{4}}+\frac{\mathrm{3x}}{\mathrm{4}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Commented by Tony Lin last updated on 09/Jun/20
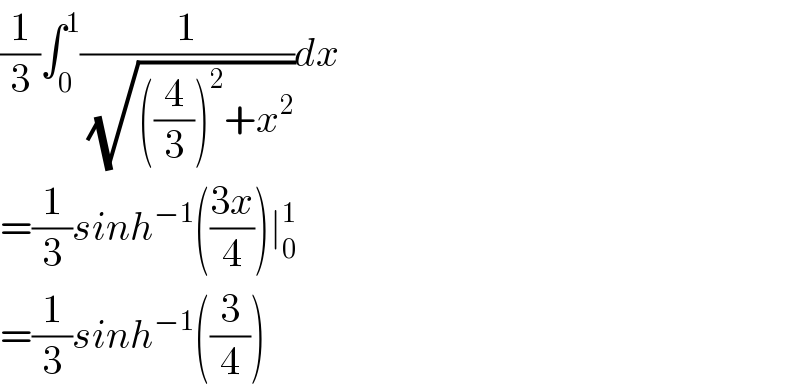
$$\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \: \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$
Commented by john santu last updated on 09/Jun/20

$$\mathrm{joosss}\:\mathrm{coolll} \\ $$
Answered by smridha last updated on 10/Jun/20
![(1/3)∫_0 ^1 (dx/( (√(((4/3))^2 +x^2 ))))=(1/3) (ln[x+(√(((4/3))^2 +x^2 ))])_0 ^1 =(1/3)ln2](https://www.tinkutara.com/question/Q97691.png)
$$\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{dx}}}{\:\sqrt{\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} +\boldsymbol{{x}}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{3}}\:\left(\boldsymbol{{ln}}\left[\boldsymbol{{x}}+\sqrt{\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} +\boldsymbol{{x}}^{\mathrm{2}} }\right]\right)_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{ln}}\mathrm{2} \\ $$
Answered by Rio Michael last updated on 09/Jun/20
![RecaLl ∫(1/( (√(x^2 +a^2 )))) dx = ln(x + (√(x^2 + a^2 ))) + c ∫_0 ^1 (1/( (√(16+ 9x^2 )))) dx = (1/3)∫_0 ^1 (1/( (√(x^2 + ((4/3))^2 ))))dx = (1/3) [ln(x + (√(x^2 +((4/3))^2 )))]_0 ^1 = (1/3)[ln((8/5))−ln((4/3))] = (1/3) ln 2](https://www.tinkutara.com/question/Q97693.png)
$$\:\mathcal{R}\mathrm{eca}\mathcal{L}{l}\:\:\int\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }}\:{dx}\:=\:\mathrm{ln}\left({x}\:+\:\sqrt{{x}^{\mathrm{2}} \:+\:{a}^{\mathrm{2}} }\right)\:+\:{c} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{16}+\:\mathrm{9}{x}^{\mathrm{2}} }}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+\:\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} }}{dx}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\left[\mathrm{ln}\left({x}\:+\:\sqrt{{x}^{\mathrm{2}} \:+\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \: \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{ln}\left(\frac{\mathrm{8}}{\mathrm{5}}\right)−\mathrm{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\right]\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{ln}\:\mathrm{2} \\ $$
Commented by peter frank last updated on 09/Jun/20

$$\mathrm{good} \\ $$
Answered by mathmax by abdo last updated on 09/Jun/20
![I =∫_0 ^1 (dx/( (√(16+9x^2 )))) ⇒I =(1/4)∫_0 ^1 (dx/( (√(1+(9/(16))x^2 )))) changement (3/4)x=t give I =(1/4)× ∫_0 ^(3/4) (1/( (√(1+t^2 ))))×(4/3) dt =(1/3)[ln(t+(√(1+t^2 ))]_0 ^(3/4) =(1/3){ln((3/4)+(√(1+(9/(16))))) =(1/3)ln((3/4) +(5/4)) =(1/3)ln(2)](https://www.tinkutara.com/question/Q97704.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{16}+\mathrm{9x}^{\mathrm{2}} }}\:\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{16}}\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{changement}\:\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{4}}×\:\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{4}}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{4}}{\mathrm{3}}\:\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{4}}} \:=\frac{\mathrm{1}}{\mathrm{3}}\left\{\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}+\sqrt{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{16}}}\right)\right.\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\:+\frac{\mathrm{5}}{\mathrm{4}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$
