Question Number 145358 by qaz last updated on 04/Jul/21
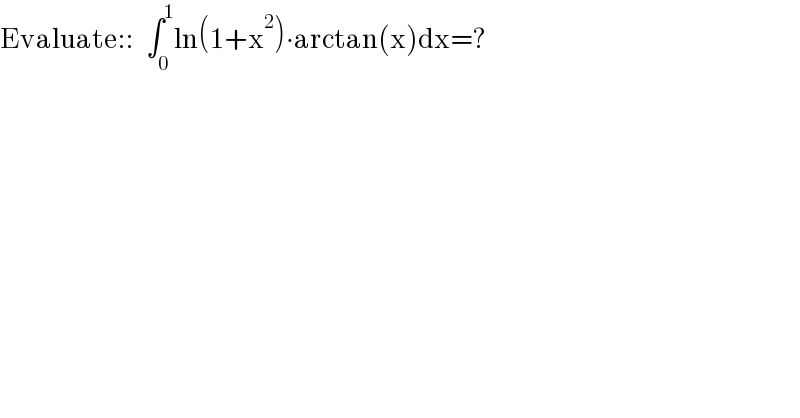
$$\mathrm{Evaluate}::\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\centerdot\mathrm{arctan}\left(\mathrm{x}\right)\mathrm{dx}=? \\ $$
Answered by Olaf_Thorendsen last updated on 04/Jul/21
![I = ∫_0 ^1 ln(1+x^2 )arctan(x) dx I = [xln(1+x^2 )arctan(x)]_0 ^1 −∫_0 ^1 x(((2x)/(1+x^2 ))arctan(x)+((ln(1+x^2 ))/(1+x^2 ))) dx I = (π/4)ln(2)−2∫_0 ^1 arctanx dx +2∫_0 ^1 ((arctanx)/(1+x^2 )) dx+∫_0 ^1 (1/2).((2x)/(1+x^2 )).ln(1+x^2 ) dx I = (π/4)ln(2)−2[xarctanx−(1/2)ln(1+x^2 )]_0 ^1 +2[(1/2)arctan^2 x]_0 ^1 +(1/4)[ln^2 (1+x^2 )]_0 ^1 I = (π/4)ln(2)−2((π/4)−(1/2)ln(2)) +(π^2 /(16))+(1/4)ln^2 (2) I =(π^2 /(16))+ (π/4)(ln(2)−2)+(1/4)ln^2 (2)+ln(2)](https://www.tinkutara.com/question/Q145374.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mathrm{arctan}\left({x}\right)\:{dx} \\ $$$$\mathrm{I}\:=\:\left[{x}\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mathrm{arctan}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{arctan}\left({x}\right)+\frac{\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{arctan}{x}\:{dx} \\ $$$$+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{arctan}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }.\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:{dx} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\left[{x}\mathrm{arctan}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$+\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\right) \\ $$$$+\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\mathrm{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\:\frac{\pi}{\mathrm{4}}\left(\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\mathrm{ln}\left(\mathrm{2}\right) \\ $$
