Question Number 48289 by Abdulhafeez Abu qatada last updated on 21/Nov/18
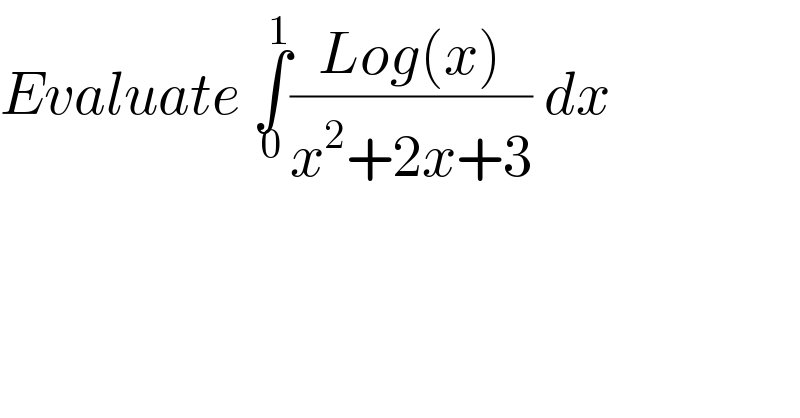
$${Evaluate}\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{Log}\left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}}\:{dx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Nov/18
Commented by maxmathsup by imad last updated on 22/Nov/18
![let A =∫_0 ^1 ((ln(x))/(x^2 +2x+3))dx ⇒A =∫_0 ^1 ((ln(x))/((x+1)^2 +2)) A =_(x+1 =(√2)t) ∫_(1/( (√2))) ^(√2) ((ln(t(√2)−1))/(2(1+t^2 ))) (√2)dt =(1/( (√2))) ∫_(1/( (√2))) ^(√2) ((ln(t(√2)−1))/(1+t^2 ))dt let consider the parametric function ϕ(x)=∫_(1/( (√2))) ^(√2) ((ln(xt−1))/(1+t^2 ))dt (xt>1) ϕ^′ (x) = ∫_(1/( (√2))) ^(√2) (t/((xt−1)(1+t^2 ))) dt let decompose F(t)=(t/((xt−1)(1+t^2 ))) F(t)=(a/(xt−1)) +((bt+c)/(t^2 +1)) a =lim_(t→(1/x)) (xt−1)F(t) =(1/(x(1+(1/x^2 )))) =(1/(x+(1/x))) =(x/(x^2 +1)) lim_(t→+∞) t F(t)=(a/x) +b ⇒b=−(1/(x^2 +1)) ⇒F(t)=(x/((x^2 +1)(xt−1))) +((−(t/(x^2 +1))+c)/(t^2 +1)) F(0) =0 =−(x/((x^2 +1))) +c ⇒c=(x/(x^2 +1)) ⇒ F(t)= (x/((x^2 +1)(xt−1))) −(1/(x^2 +1)) ((t −x)/(t^2 +1)) ⇒ ϕ^′ (x) =∫_(1/( (√2))) ^(√2) ( (x/((x^2 +1)(xt−1))) −(1/(x^2 +1)) ((t−x)/(t^2 +1)))dt =(x/(x^2 +1)) ∫_(1/( (√2))) ^(√2) (dt/(xt−1)) −(1/(2(x^2 +1))) ∫_(1/( (√2))) ^(√2) ((2t)/(t^2 +1)) +(x/(x^2 +1)) ∫_(1/( (√2))) ^(√2) (dt/(t^2 +1)) =(1/(x^2 +1))ln∣xt−1∣]_(1/( (√2))) ^(√2) −(1/(2(x^2 +1)))[ln(t^2 +1)]_(1/( (√2))) ^(√2) +(x/(x^2 +1)) [arctan(t)]_(1/( (√2))) ^(√2) =(1/(x^2 +1)){ln∣x(√2)−1∣−ln∣(x/( (√2)))−1∣}−((ln(2))/(2(x^2 +1))) +(x/(x^2 +1)) {arctan((√2))−arctan((1/( (√2))))} ⇒ ϕ(x) = ∫ ((ln(x(√2)−1))/(x^2 +1)) dx−∫ ((ln((x/( (√2)))−1))/(x^2 +1))dx −((ln(2))/2) ∫ (dx/(1+x^2 )) +(arctan((√2))−arctan((1/( (√2)))) ∫ ((xdx)/(x^2 +1))+c ⇒ ϕ(x) =∫ ((ln(x(√2)−1))/(x^2 +1))dx−∫ ((ln(x−(√2)))/(x^2 +1)) dx +ln((√2))arctanx−((ln(2))/2) arctanx +(1/2)(arctan((√2))−arctan((1/( (√2)))))ln(1+x^2 )+c =∫ ((ln(x(√2)−1))/(x^2 +1))dx−∫ ((ln(x−(√2)))/(x^2 +1))dx +(1/2)(arctan((√2))−arctan((1/( (√2)))))ln(1+x^2 )+c ....be continued...](https://www.tinkutara.com/question/Q48362.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}\:\Rightarrow{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}} \\ $$$${A}\:=_{{x}+\mathrm{1}\:=\sqrt{\mathrm{2}}{t}} \:\:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{ln}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\sqrt{\mathrm{2}}{dt}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{ln}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{let}\:{consider}\:{the} \\ $$$${parametric}\:{function}\:\varphi\left({x}\right)=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\frac{{ln}\left({xt}−\mathrm{1}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:\:\left({xt}>\mathrm{1}\right) \\ $$$$\varphi^{'} \left({x}\right)\:=\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{t}}{\left({xt}−\mathrm{1}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:{dt}\:{let}\:{decompose}\:{F}\left({t}\right)=\frac{{t}}{\left({xt}−\mathrm{1}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$${F}\left({t}\right)=\frac{{a}}{{xt}−\mathrm{1}}\:+\frac{{bt}+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow\frac{\mathrm{1}}{{x}}} \:\:\left({xt}−\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}}\:=\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)=\frac{{a}}{{x}}\:+{b}\:\Rightarrow{b}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{F}\left({t}\right)=\frac{{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xt}−\mathrm{1}\right)}\:+\frac{−\frac{{t}}{{x}^{\mathrm{2}} \:+\mathrm{1}}+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=−\frac{{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+{c}\:\Rightarrow{c}=\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({t}\right)=\:\frac{{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xt}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{{t}\:−{x}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\varphi^{'} \left({x}\right)\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \left(\:\:\frac{{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({xt}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{{t}−{x}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\right){dt} \\ $$$$=\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{dt}}{{xt}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\left.=\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{ln}\mid{xt}−\mathrm{1}\mid\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:−\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\left[{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \:\:\:+\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\left[{arctan}\left({t}\right)\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\left\{{ln}\mid{x}\sqrt{\mathrm{2}}−\mathrm{1}\mid−{ln}\mid\frac{{x}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}\mid\right\}−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$+\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\left\{{arctan}\left(\sqrt{\mathrm{2}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right\}\:\Rightarrow \\ $$$$\varphi\left({x}\right)\:=\:\int\:\:\frac{{ln}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}−\int\:\:\frac{{ln}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\int\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\: \\ $$$$+\left({arctan}\left(\sqrt{\mathrm{2}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\:\int\:\frac{{xdx}}{{x}^{\mathrm{2}} \:+\mathrm{1}}+{c}\:\Rightarrow\right. \\ $$$$\varphi\left({x}\right)\:=\int\:\frac{{ln}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}−\int\:\:\frac{{ln}\left({x}−\sqrt{\mathrm{2}}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:+{ln}\left(\sqrt{\mathrm{2}}\right){arctanx}−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:{arctanx} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\left({arctan}\left(\sqrt{\mathrm{2}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right){ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{c} \\ $$$$=\int\:\frac{{ln}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}−\int\:\frac{{ln}\left({x}−\sqrt{\mathrm{2}}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\left({arctan}\left(\sqrt{\mathrm{2}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right){ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{c} \\ $$$$….{be}\:{continued}… \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 22/Nov/18
![we have 0<x^2 <1 ,0<2x<2 ⇒ 3<x^2 +2x+3<5 ⇒ (1/5)<(1/(x^2 +2x+3)) <(1/3) ⇒ ⇒−(1/5)ln(x)<−((lnx)/(x^2 +2x+3)) <−(1/3)ln(x) ( see that ln(x)<0 on ]0,1[) ⇒ (1/3)ln(x) <((ln(x))/(x^2 +2x+3))<(1/5)ln(x) ⇒(1/3) ∫_0 ^1 ln(x)dx <∫_0 ^1 ((ln(x))/(x^2 +2x+3))dx<(1/5)∫_0 ^1 ln(x) ⇒ (1/3)[xln(x)−x]_0 ^1 <∫_0 ^1 ((ln(x))/(x^2 +2x+3))< (1/5)[xln(x)−x]_0 ^1 ⇒ −(1/3)<∫_0 ^1 ((ln(x))/(x^2 +2x+3))dx<−(1/5) we can take ∫_0 ^1 ((ln(x))/(x^2 +2x+3)) ∼−(8/(30)) with precision σ =(((1/3)−(1/5))/2) =(2/(30)) .](https://www.tinkutara.com/question/Q48364.png)
$${we}\:{have}\:\mathrm{0}<{x}^{\mathrm{2}} <\mathrm{1}\:\:,\mathrm{0}<\mathrm{2}{x}<\mathrm{2}\:\Rightarrow\:\mathrm{3}<{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}<\mathrm{5}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{5}}<\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}\:<\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{5}}{ln}\left({x}\right)<−\frac{{lnx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}\:<−\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({x}\right)\:\:\left(\:{see}\:{that}\:{ln}\left({x}\right)<\mathrm{0}\:{on}\:\right]\mathrm{0},\mathrm{1}\left[\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}{ln}\left({x}\right)\:<\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}<\frac{\mathrm{1}}{\mathrm{5}}{ln}\left({x}\right)\:\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){dx}\:<\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}<\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\left[{xln}\left({x}\right)−{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \:<\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}<\:\frac{\mathrm{1}}{\mathrm{5}}\left[{xln}\left({x}\right)−{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}<\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}<−\frac{\mathrm{1}}{\mathrm{5}}\:\:{we}\:{can}\:{take}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}\:\sim−\frac{\mathrm{8}}{\mathrm{30}} \\ $$$${with}\:{precision}\:\sigma\:=\frac{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{2}}\:=\frac{\mathrm{2}}{\mathrm{30}}\:. \\ $$
Commented by maxmathsup by imad last updated on 22/Nov/18
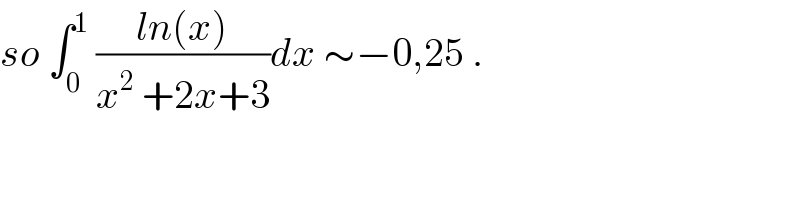
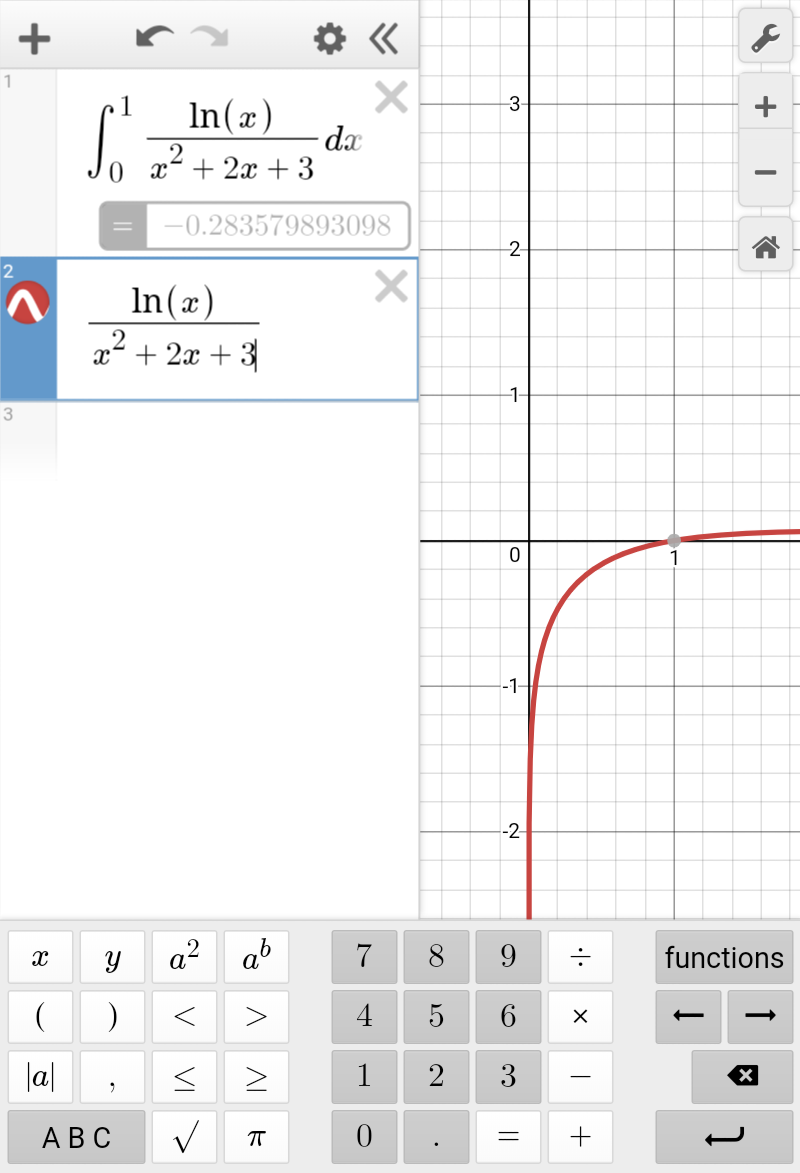
$${so}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}\:\sim−\mathrm{0},\mathrm{25}\:. \\ $$
