Question Number 89273 by Ar Brandon last updated on 16/Apr/20
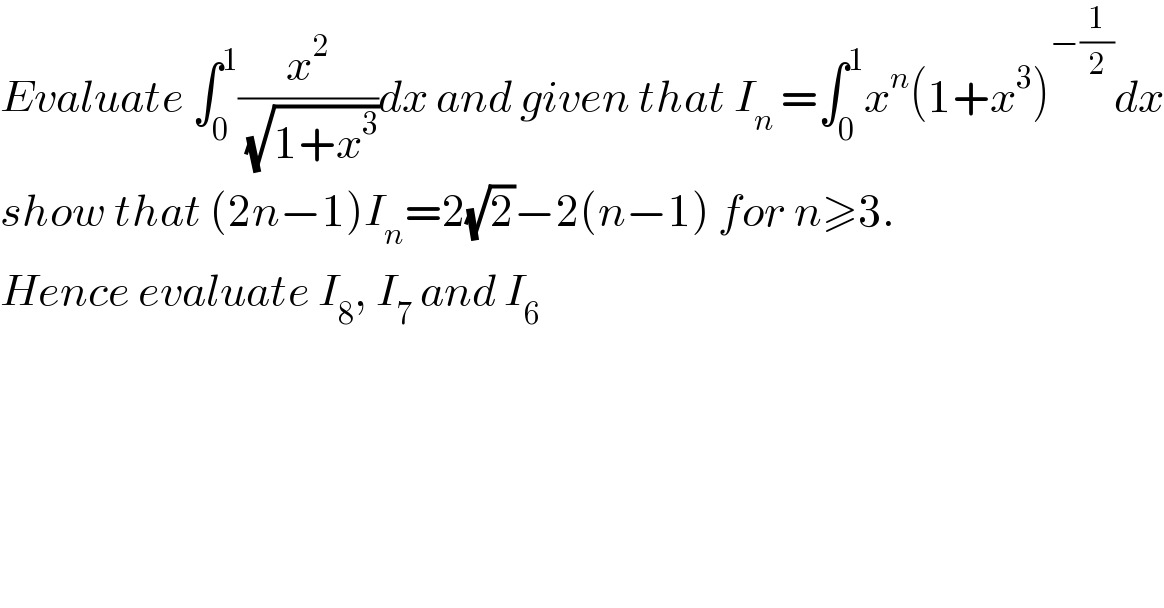
$${Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}{dx}\:{and}\:{given}\:{that}\:{I}_{{n}\:} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$${show}\:{that}\:\left(\mathrm{2}{n}−\mathrm{1}\right){I}_{{n}} =\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}\left({n}−\mathrm{1}\right)\:{for}\:{n}\geqslant\mathrm{3}. \\ $$$${Hence}\:{evaluate}\:{I}_{\mathrm{8}} ,\:{I}_{\mathrm{7}} \:{and}\:{I}_{\mathrm{6}} \\ $$
Answered by 675480065 last updated on 17/Apr/20
![evaluating the intergral: ∫_0 ^1 (x^2 /( (√(1+x^3 ))))dx=J Let u=x^3 +1 ⇒du=3x^2 dx ⇒ x^2 dx=(1/3)du. substitute above we get... J=(1/3)∫_0 ^1 u^(−(1/2)) du =(1/6)(√u), but u=(√(x^3 +1)). J=(1/6)((√(√(x^3 +1))))]_0 ^(1 ) =(1/6){(√(√2))−1} Also: I_n =∫_0 ^1 x^n (1+x^3 )^((−1)/2) dx. let u=(1+x^3 )^(−(1/2)) dv=x^n dx ⇒(du/dx)=−((3x^2 )/2)(1+x^3 )^(−(3/2)) v=(x^(n+1) /((n+1))).](https://www.tinkutara.com/question/Q89375.png)
$$ \\ $$$$ \\ $$$$\mathrm{evaluating}\:\mathrm{the}\:\mathrm{intergral}: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }}\mathrm{dx}=\mathrm{J} \\ $$$$\mathrm{Let}\:\mathrm{u}=\mathrm{x}^{\mathrm{3}} +\mathrm{1}\:\:\:\:\: \\ $$$$\:\:\Rightarrow\mathrm{du}=\mathrm{3x}^{\mathrm{2}} \mathrm{dx}\:\Rightarrow\:\mathrm{x}^{\mathrm{2}} \mathrm{dx}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{du}. \\ $$$$\mathrm{substitute}\:\mathrm{above}\:\mathrm{we}\:\mathrm{get}… \\ $$$$\mathrm{J}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{du}\:\:=\frac{\mathrm{1}}{\mathrm{6}}\sqrt{\mathrm{u}},\:\mathrm{but}\:\mathrm{u}=\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}. \\ $$$$\left.\mathrm{J}=\frac{\mathrm{1}}{\mathrm{6}}\left(\sqrt{\sqrt{\mathrm{x}^{\mathrm{3}} +\mathrm{1}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}\:} =\frac{\mathrm{1}}{\mathrm{6}}\left\{\sqrt{\sqrt{\mathrm{2}}}−\mathrm{1}\right\} \\ $$$$\mathrm{Also}: \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \mathrm{dx}. \\ $$$$\mathrm{let}\:\mathrm{u}=\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{dv}=\mathrm{x}^{\mathrm{n}} \mathrm{dx} \\ $$$$\Rightarrow\frac{\mathrm{du}}{\mathrm{dx}}=−\frac{\mathrm{3x}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\:\:\:\:\:\:\:\mathrm{v}=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{1}\right)}. \\ $$$$ \\ $$
