Question Number 174548 by mnjuly1970 last updated on 03/Aug/22
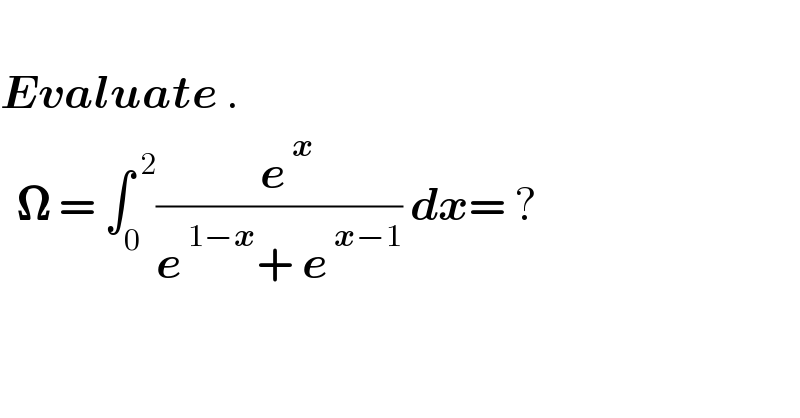
$$ \\ $$$$\boldsymbol{{Evaluate}}\:. \\ $$$$\:\:\boldsymbol{\Omega}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{2}} \frac{\:\:\boldsymbol{{e}}^{\:\boldsymbol{{x}}} }{\boldsymbol{{e}}^{\:\mathrm{1}−\boldsymbol{{x}}} +\:\boldsymbol{{e}}^{\:\boldsymbol{{x}}−\mathrm{1}} }\:\boldsymbol{{dx}}=\:? \\ $$$$\:\:\:\: \\ $$
Answered by CElcedricjunior last updated on 03/Aug/22
![Ω=∫_0 ^2 (e^x /(e^(1−x) +e^(x−1) ))dx=∫_0 ^2 ((e^(x−1) ×e^x dx)/(1+e^(x−1) ×e^(x−1) )) =∫_0 ^2 (e^(2x−1) /(1+e^(2x−2) ))dx=(e/2)∫_0 ^2 ((2e^(2x−2) )/(1+e^(2x−2) ))dx 𝛀=(e/2)[ln(1+e^(2x−2) )]_0 ^2 =(e/2)[ln(1+e^2 )−ln(1+e^(−2) )] =(e/2)lne^2 𝛀=e ..........le ce^� le^� bre cedric junior............](https://www.tinkutara.com/question/Q174555.png)
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} }{\boldsymbol{\mathrm{e}}^{\mathrm{1}−\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}−\mathrm{1}} }\boldsymbol{\mathrm{dx}}=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\boldsymbol{{e}}^{\boldsymbol{{x}}−\mathrm{1}} ×\boldsymbol{{e}}^{\boldsymbol{{x}}} \boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{e}}^{\boldsymbol{{x}}−\mathrm{1}} ×\boldsymbol{{e}}^{\boldsymbol{{x}}−\mathrm{1}} } \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}−\mathrm{1}} }{\mathrm{1}+\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}−\mathrm{2}} }\boldsymbol{{dx}}=\frac{\boldsymbol{{e}}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}−\mathrm{2}} }{\mathrm{1}+\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}−\mathrm{2}} }\boldsymbol{{dx}} \\ $$$$\boldsymbol{\Omega}=\frac{\boldsymbol{{e}}}{\mathrm{2}}\left[\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{e}}^{\mathrm{2}\boldsymbol{\mathrm{x}}−\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{2}} =\frac{\boldsymbol{\mathrm{e}}}{\mathrm{2}}\left[\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{e}}^{\mathrm{2}} \right)−\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\overset{−\mathrm{2}} {\boldsymbol{\mathrm{e}}}\right)\right] \\ $$$$=\frac{\boldsymbol{\mathrm{e}}}{\mathrm{2}}\boldsymbol{\mathrm{lne}}^{\mathrm{2}} \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{e}} \\ $$$$……….{le}\:{c}\acute {{e}l}\grave {{e}bre}\:{cedric}\:\:{junior}………… \\ $$
