Question Number 118073 by bemath last updated on 15/Oct/20

$$\mathrm{Evaluate}\:\underset{\mathrm{0}} {\overset{{a}} {\int}}\:{b}\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:{dx}\: \\ $$
Answered by john santu last updated on 15/Oct/20

$${I}=\underset{\mathrm{0}} {\overset{{a}} {\int}}\:\frac{{b}}{{a}}\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:{dx}\:;\:{the}\:{integral}\:{represents}\:{the}\:{area} \\ $$$${of}\:{a}\:{quarter}\:{circle}\:{having}\:{radius}\:{a} \\ $$$${I}=\:\frac{{b}}{{a}}×\frac{\mathrm{1}}{\mathrm{4}}\pi{a}^{\mathrm{2}} \:=\:\frac{\pi{ab}}{\mathrm{4}} \\ $$
Commented by bemath last updated on 15/Oct/20

$$\mathrm{gave}\:\mathrm{kudos} \\ $$
Commented by MJS_new last updated on 15/Oct/20
$$\mathrm{right}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{but}\:\mathrm{an}\:\mathrm{ellipse} \\ $$
Commented by john santu last updated on 16/Oct/20

$${no}\:{sir}.\:{its}\:{a}\:{circle}.\:{If}\:{y}\:=\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\: \\ $$$$\Rightarrow{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} \: \\ $$
Commented by MJS_new last updated on 16/Oct/20
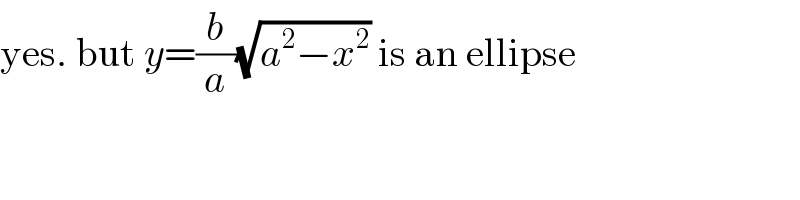
$$\mathrm{yes}.\:\mathrm{but}\:{y}=\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{an}\:\mathrm{ellipse} \\ $$
Answered by 1549442205PVT last updated on 15/Oct/20
![Evaluate ∫_0 ^a b(√(1−(x^2 /a^2 ))) dx Put x=acosϕ(ϕ∈[0,π])⇒dx=−asinϕdϕ I=−∫_(π/2) ^( 0) absin^2 ϕdϕ=∫_0 ^( π/2) ab((1−cos2ϕ)/2)dϕ =(((abϕ)/2)−((ab)/4)sin2ϕ)∣_0 ^(π/2) =((abπ)/( 4))](https://www.tinkutara.com/question/Q118093.png)
$$\mathrm{Evaluate}\:\underset{\mathrm{0}} {\overset{{a}} {\int}}\:{b}\sqrt{\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}\:{dx}\: \\ $$$$\mathrm{Put}\:\mathrm{x}=\mathrm{acos}\varphi\left(\varphi\in\left[\mathrm{0},\pi\right]\right)\Rightarrow\mathrm{dx}=−\mathrm{asin}\varphi\mathrm{d}\varphi \\ $$$$\mathrm{I}=−\int_{\pi/\mathrm{2}} ^{\:\mathrm{0}} \mathrm{absin}^{\mathrm{2}} \varphi\mathrm{d}\varphi=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \mathrm{ab}\frac{\mathrm{1}−\mathrm{cos2}\varphi}{\mathrm{2}}\mathrm{d}\varphi \\ $$$$=\left(\frac{\mathrm{ab}\varphi}{\mathrm{2}}−\frac{\mathrm{ab}}{\mathrm{4}}\mathrm{sin2}\varphi\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} =\frac{\mathrm{ab}\pi}{\:\mathrm{4}} \\ $$
