Question Number 83164 by niroj last updated on 28/Feb/20
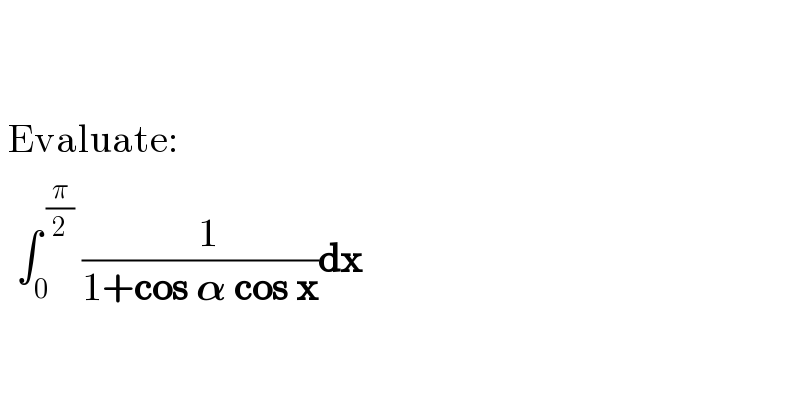
$$ \\ $$$$ \\ $$$$\:\mathrm{Evaluate}: \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\:\:\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{cos}}\:\boldsymbol{\alpha}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}} \\ $$
Commented by mathmax by abdo last updated on 28/Feb/20
![let I =∫_0 ^(π/2) (dx/(1+cosα cosx)) changement tan((x/2))=t give I =∫_0 ^1 (1/(1+cosα×((1−t^2 )/(1+t^2 ))))((2dt)/(1+t^2 )) =2∫_0 ^1 (dt/(1+t^2 +cosα(1−t^2 ))) =2 ∫_0 ^1 (dt/((1−cosα)t^2 +1+cosα)) =(2/(1−cosα)) ∫_0 ^1 (dt/(t^2 +((1+cosα)/(1−cosα)))) =(2/(1−cosα))∫_0 ^1 (dt/(t^2 +tan^2 ((α/2)))) =_(t=∣tan((α/2))∣u) (2/(1−cosα))∫_0 ^(∣cotan((α/2))∣) ((∣tan((α/2))∣du)/(tan^2 ((α/2))(1+u^2 ))) =(2/((1−cosα)∣tan((α/2))∣)) [arctanu]_0 ^(∣(1/(tan((α/2))))∣) I=(2/((1−cosα)∣tan((α/2))∣)) arctan(∣(1/(tan((α/2))))∣) case 1 tan((α/2))>0 ⇒I =((2cos((α/2)))/(2sin^2 ((α/2))×sin((α/2))))((π/2)−(α/2)) =((cos((α/2)))/(sin^3 ((α/2))))×(((π−α)/2)) case2 tan((α/2))<0 ⇒ I =−((cos((α/2)))/(sin^3 ((α/2))))×(−arctan((1/(tan((α/2))))) =((cos((α/2)))/(sin^3 ((α/2))))(−(π/2)−(α/2)) =−((cos((α/2)))/(sin^3 ((α/2))))(((π+α)/2))](https://www.tinkutara.com/question/Q83176.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{1}+{cos}\alpha\:{cosx}}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}+{cos}\alpha×\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +{cos}\alpha\left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left(\mathrm{1}−{cos}\alpha\right){t}^{\mathrm{2}} \:+\mathrm{1}+{cos}\alpha}\:=\frac{\mathrm{2}}{\mathrm{1}−{cos}\alpha}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+{cos}\alpha}{\mathrm{1}−{cos}\alpha}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−{cos}\alpha}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+{tan}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)}\:=_{{t}=\mid{tan}\left(\frac{\alpha}{\mathrm{2}}\right)\mid{u}} \frac{\mathrm{2}}{\mathrm{1}−{cos}\alpha}\int_{\mathrm{0}} ^{\mid{cotan}\left(\frac{\alpha}{\mathrm{2}}\right)\mid} \frac{\mid{tan}\left(\frac{\alpha}{\mathrm{2}}\right)\mid{du}}{{tan}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}−{cos}\alpha\right)\mid{tan}\left(\frac{\alpha}{\mathrm{2}}\right)\mid}\:\left[{arctanu}\right]_{\mathrm{0}} ^{\mid\frac{\mathrm{1}}{{tan}\left(\frac{\alpha}{\mathrm{2}}\right)}\mid} \\ $$$${I}=\frac{\mathrm{2}}{\left(\mathrm{1}−{cos}\alpha\right)\mid{tan}\left(\frac{\alpha}{\mathrm{2}}\right)\mid}\:{arctan}\left(\mid\frac{\mathrm{1}}{{tan}\left(\frac{\alpha}{\mathrm{2}}\right)}\mid\right) \\ $$$${case}\:\mathrm{1}\:\:{tan}\left(\frac{\alpha}{\mathrm{2}}\right)>\mathrm{0}\:\Rightarrow{I}\:=\frac{\mathrm{2}{cos}\left(\frac{\alpha}{\mathrm{2}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)×{sin}\left(\frac{\alpha}{\mathrm{2}}\right)}\left(\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\frac{{cos}\left(\frac{\alpha}{\mathrm{2}}\right)}{{sin}^{\mathrm{3}} \left(\frac{\alpha}{\mathrm{2}}\right)}×\left(\frac{\pi−\alpha}{\mathrm{2}}\right) \\ $$$${case}\mathrm{2}\:{tan}\left(\frac{\alpha}{\mathrm{2}}\right)<\mathrm{0}\:\Rightarrow\:{I}\:=−\frac{{cos}\left(\frac{\alpha}{\mathrm{2}}\right)}{{sin}^{\mathrm{3}} \left(\frac{\alpha}{\mathrm{2}}\right)}×\left(−{arctan}\left(\frac{\mathrm{1}}{{tan}\left(\frac{\alpha}{\mathrm{2}}\right)}\right)\right. \\ $$$$=\frac{{cos}\left(\frac{\alpha}{\mathrm{2}}\right)}{{sin}^{\mathrm{3}} \left(\frac{\alpha}{\mathrm{2}}\right)}\left(−\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right)\:=−\frac{{cos}\left(\frac{\alpha}{\mathrm{2}}\right)}{{sin}^{\mathrm{3}} \left(\frac{\alpha}{\mathrm{2}}\right)}\left(\frac{\pi+\alpha}{\mathrm{2}}\right) \\ $$
Commented by niroj last updated on 28/Feb/20
$$\:\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\:\mathrm{of}\:\mathrm{you}. \\ $$
Answered by mr W last updated on 28/Feb/20
![(1/(1+cos α cos x)) =(1/(cos α))×(1/((1/(cos α))+cos x)) let a=(1/(cos α)) ≥1 or ≤−1 ∫_0 ^( (π/2)) (( 1)/(1+cos 𝛂 cos x))dx =a∫_0 ^(π/2) (dx/(a+cos x)) =((2a)/( (√(a^2 −1))))[tan^(−1) (((√(a−1))/( (√(a+1))))tan (x/2))]_0 ^(π/2) =((2a)/( (√(a^2 −1))))×tan^(−1) (((√(a−1))/( (√(a+1))))) =(2/( (√(1−(1/a^2 )))))×tan^(−1) (((√(1−(1/a)))/( (√(1+(1/a)))))) =(2/( (√(1−cos^2 α))))×tan^(−1) (((√(1−cos α))/( (√(1+cos α))))) =(2/(sin α))×tan^(−1) (((√(1−1+2 sin^2 (α/2)))/( (√(1+2 cos^2 (α/2)−1))))) =(2/(sin α))×tan^(−1) (tan (α/2)) =(2/(sin α))×(α/2) =(α/(sin α))](https://www.tinkutara.com/question/Q83180.png)
$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\alpha\:\mathrm{cos}\:{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}+\mathrm{cos}\:{x}} \\ $$$${let}\:{a}=\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}\:\geqslant\mathrm{1}\:{or}\:\leqslant−\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{\:\:\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{cos}}\:\boldsymbol{\alpha}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}} \\ $$$$={a}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{a}+\mathrm{cos}\:{x}} \\ $$$$=\frac{\mathrm{2}{a}}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{{a}−\mathrm{1}}}{\:\sqrt{{a}+\mathrm{1}}}\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}{a}}{\:\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}}×\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{{a}−\mathrm{1}}}{\:\sqrt{{a}+\mathrm{1}}}\right) \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}}×\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{a}}}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{a}}}}\right) \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha}}×\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}−\mathrm{cos}\:\alpha}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:\alpha}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{sin}\:\alpha}×\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}−\mathrm{1}+\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}}}{\:\sqrt{\mathrm{1}+\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}−\mathrm{1}}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{sin}\:\alpha}×\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{sin}\:\alpha}×\frac{\alpha}{\mathrm{2}} \\ $$$$=\frac{\alpha}{\mathrm{sin}\:\alpha} \\ $$
Answered by TANMAY PANACEA last updated on 28/Feb/20
![∫_0 ^(π/2) (dx/(cosα((1/(cosα))+cosx))) [(1/(cosα))=a ] (1/(cosα))∫_0 ^(π/2) (dx/(a+cosx)) (1/(cosα))∫_0 ^(π/2) (dx/(a+((1−tan^2 (x/2))/(1+tan^2 (x/2))))) (1/(cosα))∫_0 ^(π/2) ((sec^2 (x/2))/((a+1)+tan^2 (x/2)×(a−1)))dx (1/(cosα))×(1/(a−1))∫_0 ^(π/2) ((sec^2 (x/2))/(((a+1)/(a−1))+tan^2 (x/2)))dx (1/(cosα))×(1/((1/(cosα))−1))∫_0 ^(π/2) ((sec^2 (x/2))/(((1+cosα)/(1−cosα))+tan^2 (x/2)))dx (1/(1−cosα))∫_0 ^(π/2) ((d(tan(x/2))×2)/(cot^2 (α/2)+tan^2 (x/2))) (2/(2sin^2 (α/2)))×(1/(cot(α/2)))×∣tan^(−1) (((tan(x/2))/(cot(α/2))))∣_0 ^(π/2) (2/(sinα))×tan^(−1) ((1/(cot(α/2))))=(2/(sinα))×(α/2)=(α/(sinα)) pls check...](https://www.tinkutara.com/question/Q83184.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{cos}\alpha\left(\frac{\mathrm{1}}{{cos}\alpha}+{cosx}\right)}\:\:\:\left[\frac{\mathrm{1}}{{cos}\alpha}={a}\:\:\right] \\ $$$$\frac{\mathrm{1}}{{cos}\alpha}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{a}+{cosx}} \\ $$$$\frac{\mathrm{1}}{{cos}\alpha}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{a}+\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\frac{\mathrm{1}}{{cos}\alpha}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\left({a}+\mathrm{1}\right)+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\left({a}−\mathrm{1}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{{cos}\alpha}×\frac{\mathrm{1}}{{a}−\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\frac{\mathrm{1}}{{cos}\alpha}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{{cos}\alpha}−\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\frac{\mathrm{1}+{cos}\alpha}{\mathrm{1}−{cos}\alpha}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{cos}\alpha}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tan}\frac{{x}}{\mathrm{2}}\right)×\mathrm{2}}{{cot}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}}{\mathrm{2}{sin}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}}×\frac{\mathrm{1}}{{cot}\frac{\alpha}{\mathrm{2}}}×\mid{tan}^{−\mathrm{1}} \left(\frac{{tan}\frac{{x}}{\mathrm{2}}}{{cot}\frac{\alpha}{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}}{{sin}\alpha}×{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{cot}\frac{\alpha}{\mathrm{2}}}\right)=\frac{\mathrm{2}}{\boldsymbol{{sin}}\alpha}×\frac{\alpha}{\mathrm{2}}=\frac{\alpha}{{sin}\alpha} \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}… \\ $$
Commented by niroj last updated on 28/Feb/20

$$\:\mathrm{great}\:\mathrm{dear}… \\ $$
Commented by TANMAY PANACEA last updated on 28/Feb/20

$${thank}\:{you}\:{sir} \\ $$
