Question Number 14395 by tawa tawa last updated on 31/May/17
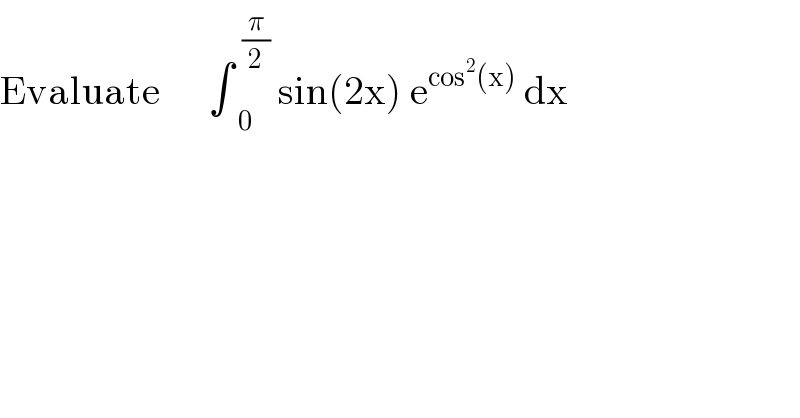
$$\mathrm{Evaluate}\:\:\:\:\:\:\int_{\:\:\:\mathrm{0}} ^{\:\:\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}\left(\mathrm{2x}\right)\:\mathrm{e}^{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)} \:\mathrm{dx}\: \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 31/May/17
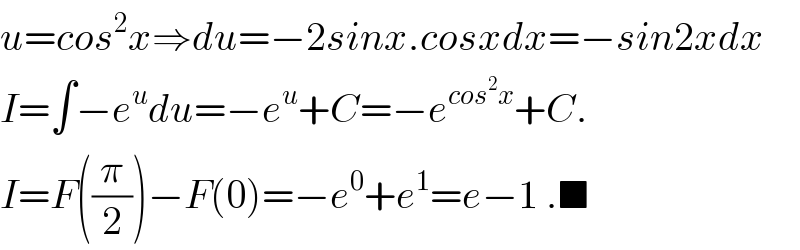
$${u}={cos}^{\mathrm{2}} {x}\Rightarrow{du}=−\mathrm{2}{sinx}.{cosxdx}=−{sin}\mathrm{2}{xdx} \\ $$$${I}=\int−{e}^{{u}} {du}=−{e}^{{u}} +{C}=−{e}^{{cos}^{\mathrm{2}} {x}} +{C}. \\ $$$${I}={F}\left(\frac{\pi}{\mathrm{2}}\right)−{F}\left(\mathrm{0}\right)=−{e}^{\mathrm{0}} +{e}^{\mathrm{1}} ={e}−\mathrm{1}\:.\blacksquare \\ $$
Commented by tawa tawa last updated on 31/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
