Question Number 118278 by Lordose last updated on 16/Oct/20
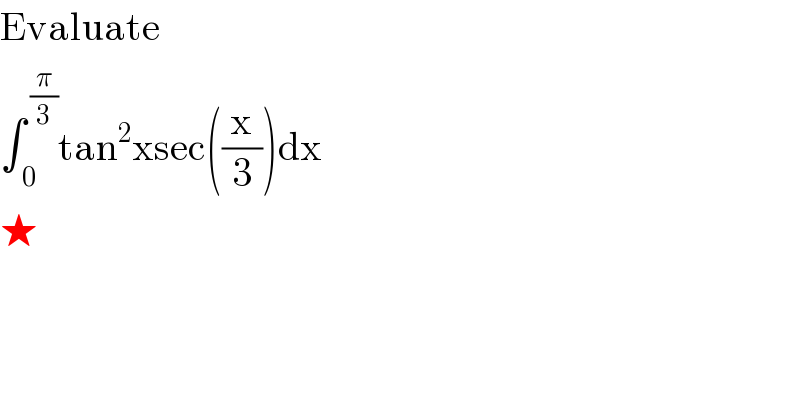
$$\mathrm{Evaluate} \\ $$$$\int_{\:\mathrm{0}} ^{\:\frac{\pi}{\mathrm{3}}} \mathrm{tan}^{\mathrm{2}} \mathrm{xsec}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\mathrm{dx} \\ $$$$\bigstar \\ $$
Answered by MJS_new last updated on 16/Oct/20
![∫tan^2 x sec (x/3) dx= [t=csc (x/3) → dx=−3tan (x/3) sin (x/3)] =−3∫(((3t^2 −4)^2 )/((t−2)^2 (t−1)^2 (t+1)^2 (t+2)^2 ))dt= =−(4/3)∫(dt/((t−2)^2 ))+(2/9)∫(dt/(t−2))−(1/(12))∫(dt/((t−1)^2 ))+((35)/(36))∫(dt/(t−1))− −(1/(12))∫(dt/((t+1)^2 ))−((35)/(36))∫(dt/(t+1))−(4/3)∫(dt/((t+2)^2 ))−(2/9)∫(dt/(t+2))= ... =((t(17t^2 −20))/(6(t^4 −5t^2 +4)))+(2/9)ln ∣((t−2)/(t+2))∣ +((35)/(36))ln ∣((t−1)/(t+1))∣ now put t=csc (x/3) I don′t think we get a useable exact value. I get ≈.713844](https://www.tinkutara.com/question/Q118302.png)
$$\int\mathrm{tan}^{\mathrm{2}} \:{x}\:\mathrm{sec}\:\frac{{x}}{\mathrm{3}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{csc}\:\frac{{x}}{\mathrm{3}}\:\rightarrow\:{dx}=−\mathrm{3tan}\:\frac{{x}}{\mathrm{3}}\:\mathrm{sin}\:\frac{{x}}{\mathrm{3}}\right] \\ $$$$=−\mathrm{3}\int\frac{\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} }{\left({t}−\mathrm{2}\right)^{\mathrm{2}} \left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{2}} }{dt}= \\ $$$$=−\frac{\mathrm{4}}{\mathrm{3}}\int\frac{{dt}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{dt}}{{t}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{12}}\int\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{35}}{\mathrm{36}}\int\frac{{dt}}{{t}−\mathrm{1}}− \\ $$$$\:\:\:−\frac{\mathrm{1}}{\mathrm{12}}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{35}}{\mathrm{36}}\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{4}}{\mathrm{3}}\int\frac{{dt}}{\left({t}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{9}}\int\frac{{dt}}{{t}+\mathrm{2}}= \\ $$$$… \\ $$$$=\frac{{t}\left(\mathrm{17}{t}^{\mathrm{2}} −\mathrm{20}\right)}{\mathrm{6}\left({t}^{\mathrm{4}} −\mathrm{5}{t}^{\mathrm{2}} +\mathrm{4}\right)}+\frac{\mathrm{2}}{\mathrm{9}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\mid\:+\frac{\mathrm{35}}{\mathrm{36}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid \\ $$$$\mathrm{now}\:\mathrm{put}\:{t}=\mathrm{csc}\:\frac{{x}}{\mathrm{3}} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{useable}\:\mathrm{exact}\:\mathrm{value}. \\ $$$$\mathrm{I}\:\mathrm{get}\:\approx.\mathrm{713844} \\ $$
