Question Number 188511 by universe last updated on 02/Mar/23
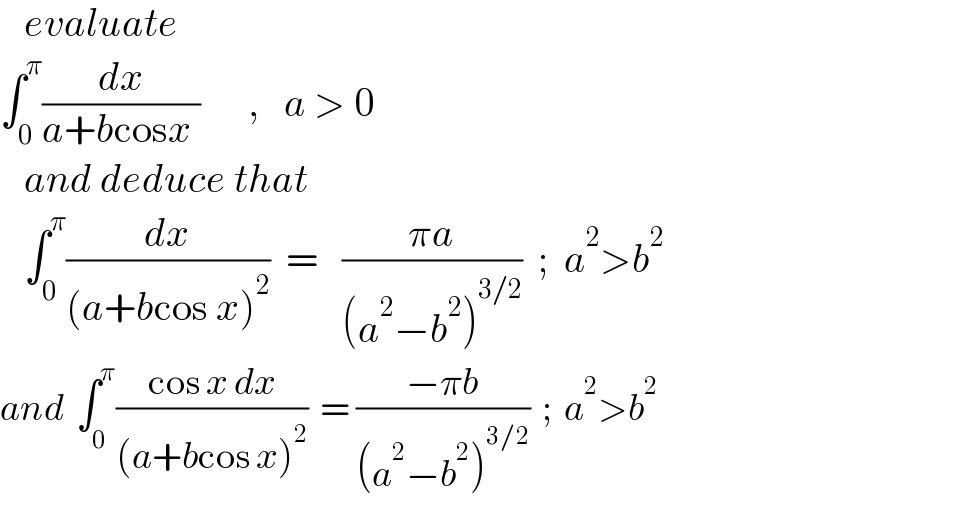
$$\:\:\:{evaluate} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{{a}+{b}\mathrm{cos}{x}\:}\:\:\:\:\:\:,\:\:\:{a}\:>\:\mathrm{0} \\ $$$$\:\:\:{and}\:{deduce}\:{that} \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left({a}+{b}\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:\:=\:\:\:\frac{\pi{a}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\:\:;\:\:{a}^{\mathrm{2}} >{b}^{\mathrm{2}} \\ $$$${and}\:\:\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{cos}\:{x}\:{dx}}{\left({a}+{b}\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:\:=\:\frac{−\pi{b}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\:\:;\:\:{a}^{\mathrm{2}} >{b}^{\mathrm{2}} \\ $$
