Question Number 126344 by mnjuly1970 last updated on 19/Dec/20
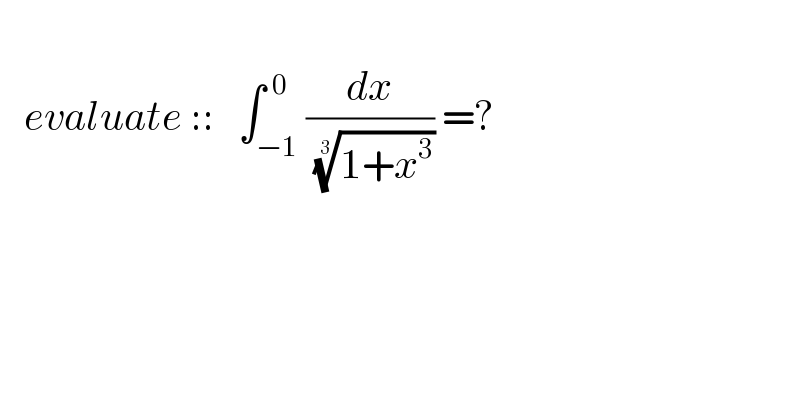
$$\:\:\:\:\: \\ $$$$\:\:\:{evaluate}\:::\:\:\:\int_{−\mathrm{1}} ^{\:\:\mathrm{0}} \frac{{dx}}{\:\sqrt[{\mathrm{3}}]{\mathrm{1}+{x}^{\mathrm{3}} }}\:=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 19/Dec/20
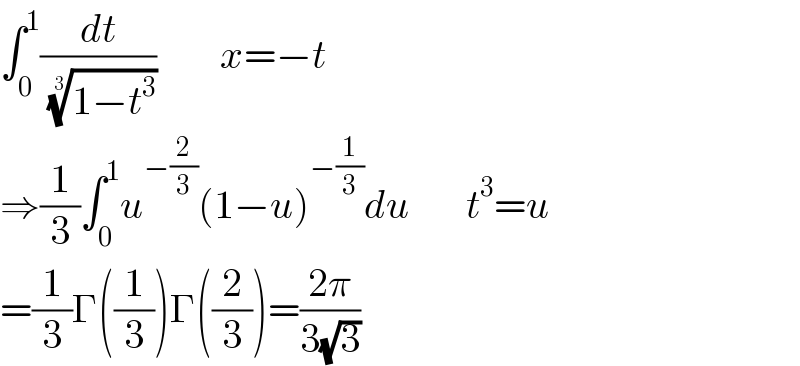
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\:\sqrt[{\mathrm{3}}]{\mathrm{1}−{t}^{\mathrm{3}} }}\:\:\:\:\:\:\:\:{x}=−{t} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} {du}\:\:\:\:\:\:\:{t}^{\mathrm{3}} ={u}\:\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by mnjuly1970 last updated on 19/Dec/20

$${thanks}\:{alot}\:{mr}\:{payan}… \\ $$
