Evaluate-1-1-2-3-3-2-3-4-5-3-4-5-2n-1-n-n-1-n-2-

Question Number 103648 by Lordose last updated on 16/Jul/20

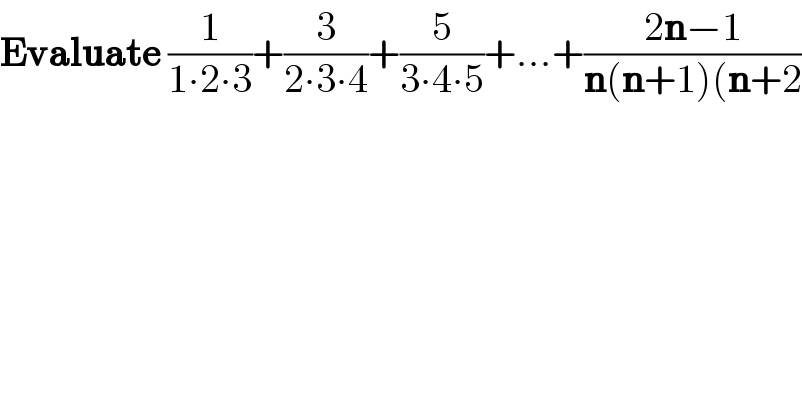
$$\boldsymbol{\mathrm{Evaluate}}\:\frac{\mathrm{1}}{\mathrm{1}\centerdot\mathrm{2}\centerdot\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}\centerdot\mathrm{3}\centerdot\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{3}\centerdot\mathrm{4}\centerdot\mathrm{5}}+…+\frac{\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}}{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}+\mathrm{2}\right.} \\ $$

Answered by Dwaipayan Shikari last updated on 16/Jul/20

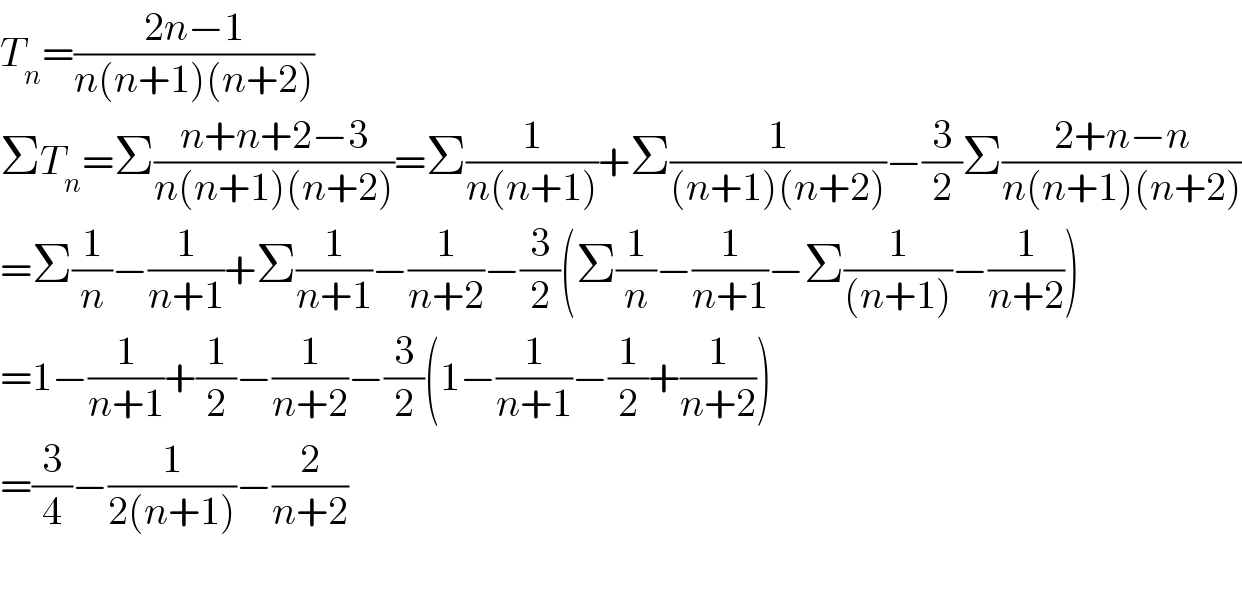
T_n =((2n−1)/(n(n+1)(n+2))) ΣT_n =Σ((n+n+2−3)/(n(n+1)(n+2)))=Σ(1/(n(n+1)))+Σ(1/((n+1)(n+2)))−(3/2)Σ((2+n−n)/(n(n+1)(n+2))) =Σ(1/n)−(1/(n+1))+Σ(1/(n+1))−(1/(n+2))−(3/2)(Σ(1/n)−(1/(n+1))−Σ(1/((n+1)))−(1/(n+2))) =1−(1/(n+1))+(1/2)−(1/(n+2))−(3/2)(1−(1/(n+1))−(1/2)+(1/(n+2))) =(3/4)−(1/(2(n+1)))−(2/(n+2))

$${T}_{{n}} =\frac{\mathrm{2}{n}−\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$\Sigma{T}_{{n}} =\Sigma\frac{{n}+{n}+\mathrm{2}−\mathrm{3}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\Sigma\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}+\Sigma\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}−\frac{\mathrm{3}}{\mathrm{2}}\Sigma\frac{\mathrm{2}+{n}−{n}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$=\Sigma\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\Sigma\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\left(\Sigma\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\Sigma\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{2}}{{n}+\mathrm{2}} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 16/Jul/20

let A_n =Σ_(k=1) ^n ((2k−1)/(k(k+1)(k+2))) ⇒ let decompose F(x) =((2x−1)/(x(x+1)(x+2))) ⇒F(x) =(a/x)+(b/(x+1)) +(c/(x+2)) a =−(1/2) , b =((−3)/(−1)) =3 ,c =((−5)/((−2)(−1))) =−(5/2) ⇒F(x)=−(1/(2x))+(3/(x+1))−(5/(2(x+2))) ⇒A_n =Σ_(k=1) ^n F(k) =−(1/2)Σ_(k=1) ^n (1/k) +3Σ_(k=1) ^n (1/(k+1))−(5/2)Σ_(k=1) ^n (1/(k+2)) Σ_(k=1) ^n (1/k) =H_n Σ_(k=1) ^n (1/(k+1)) =Σ_(k=2) ^(n+1) (1/k) =Σ_(k=1) ^n (1/k) +(1/(n+1))−1 Σ_(k=1) ^n (1/(k+2)) =Σ_(k=3) ^(n+2) (1/k) =Σ_(k=1) ^n (1/k) +(1/(n+2))−(3/2) ⇒ A_n =−(1/2)H_n +3(H_n +(1/(n+1))−1)−(5/2)(H_n +(1/(n+2))−(3/2)) =−(1/2)H_n +3H_n −(5/2) H_n +(3/(n+1))−3 −(5/(2(n+2))) +((15)/4) =(3/(n+1))−(5/(2(n+2))) +((15)/4)−3 =(3/(n+1))−(5/(2(n+2))) +(3/4)

$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{2k}−\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{2}} \\ $$$$\mathrm{a}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:,\:\mathrm{b}\:=\frac{−\mathrm{3}}{−\mathrm{1}}\:=\mathrm{3}\:\:,\mathrm{c}\:=\frac{−\mathrm{5}}{\left(−\mathrm{2}\right)\left(−\mathrm{1}\right)}\:=−\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{3}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{5}}{\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$\Rightarrow\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{F}\left(\mathrm{k}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\:+\mathrm{3}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{5}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\mathrm{H}_{\mathrm{n}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\:=\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\mathrm{1} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\:=\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}+\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} +\mathrm{3}\left(\mathrm{H}_{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\mathrm{1}\right)−\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{H}_{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} \:+\mathrm{3H}_{\mathrm{n}} −\frac{\mathrm{5}}{\mathrm{2}}\:\mathrm{H}_{\mathrm{n}} \:+\frac{\mathrm{3}}{\mathrm{n}+\mathrm{1}}−\mathrm{3}\:−\frac{\mathrm{5}}{\mathrm{2}\left(\mathrm{n}+\mathrm{2}\right)}\:+\frac{\mathrm{15}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{5}}{\mathrm{2}\left(\mathrm{n}+\mathrm{2}\right)}\:+\frac{\mathrm{15}}{\mathrm{4}}−\mathrm{3}\:=\frac{\mathrm{3}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{5}}{\mathrm{2}\left(\mathrm{n}+\mathrm{2}\right)}\:+\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Facebook Tweet Pin

Evaluate-1-1-2-3-3-2-3-4-5-3-4-5-2n-1-n-n-1-n-2-

Leave a Reply Cancel reply