Question Number 170519 by nimnim last updated on 25/May/22
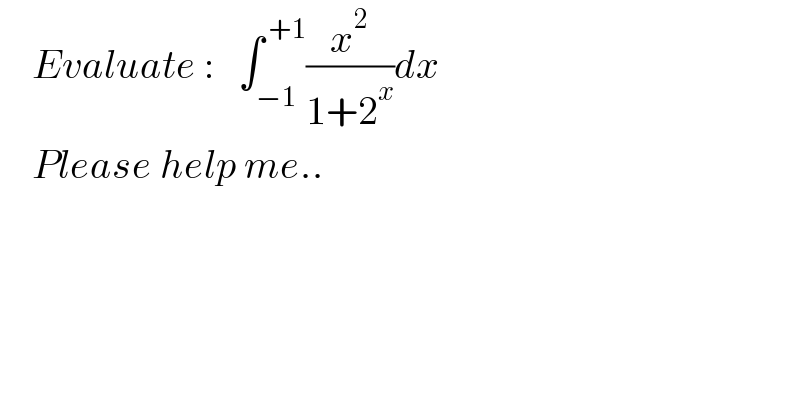
$$\:\:\:\:{Evaluate}\::\:\:\:\int_{−\mathrm{1}} ^{\:+\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}^{{x}} }{dx} \\ $$$$\:\:\:\:{Please}\:{help}\:{me}.. \\ $$
Answered by Mathspace last updated on 26/May/22
![I=∫_(−1) ^1 (x^2 /(1+2^x ))dx ⇒I=_(x=−t) ∫_1 ^(−1) (t^2 /(1+2^(−t) ))(−dt)=∫_(−1) ^1 (x^2 /(1+2^(−x) ))dx ⇒ 2I=∫_(−1) ^1 ((1/(1+2^x ))+(1/(1+2^(−x) )))x^2 dx =∫_(−1) ^1 ((1+2^(−x) +1+2^x )/(1+2^(−x) +2^x +1))x^2 dx =∫_(−1) ^1 x^2 dx=[(x^3 /3)]_(−1) ^1 =(1/3)+(1/3) =(2/3)](https://www.tinkutara.com/question/Q170553.png)
$${I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}^{{x}} }{dx}\:\Rightarrow{I}=_{{x}=−{t}} \\ $$$$\int_{\mathrm{1}} ^{−\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}^{−{t}} }\left(−{dt}\right)=\int_{−\mathrm{1}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2}^{−{x}} }{dx}\:\Rightarrow \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{{x}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−{x}} }\right){x}^{\mathrm{2}} {dx} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}+\mathrm{2}^{−{x}} +\mathrm{1}+\mathrm{2}^{{x}} }{\mathrm{1}+\mathrm{2}^{−{x}} +\mathrm{2}^{{x}} +\mathrm{1}}{x}^{\mathrm{2}} {dx} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} {x}^{\mathrm{2}} {dx}=\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{−\mathrm{1}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by Mathspace last updated on 26/May/22

$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by SLVR last updated on 27/May/22

$${nice}\:{solution} \\ $$
Commented by nimnim last updated on 27/May/22

$${Thank}\:{you}\:{Sir}. \\ $$
