Menu Close

Evaluate-1-2-3-8-3-16-5-64-

Tinku Tara 0 Comments
Pin




Question Number 104406 by Don08q last updated on 21/Jul/20
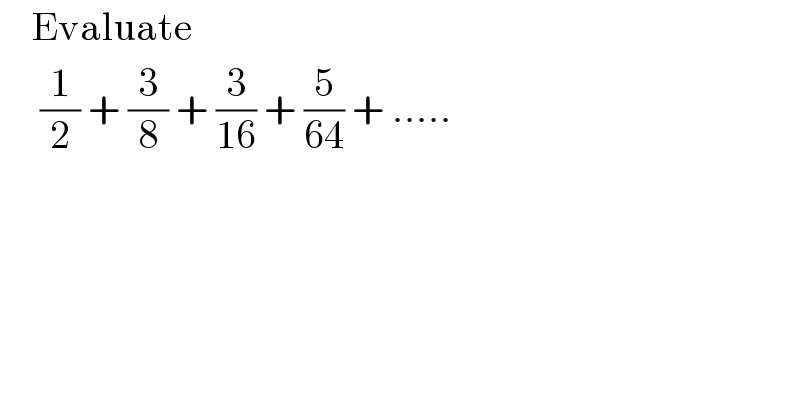
Evaluate (1/2) + (3/8) + (3/(16)) + (5/(64)) + .....
$$\:\:\:\:\mathrm{Evaluate} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{8}}\:+\:\frac{\mathrm{3}}{\mathrm{16}}\:+\:\frac{\mathrm{5}}{\mathrm{64}}\:+\:….. \\ $$
Commented by Don08q last updated on 21/Jul/20
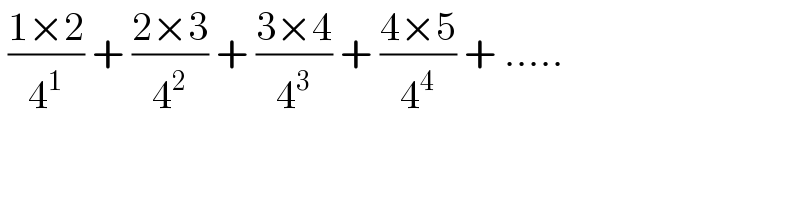
((1×2)/4^1 ) + ((2×3)/4^2 ) + ((3×4)/4^3 ) + ((4×5)/4^4 ) + .....
$$\:\frac{\mathrm{1}×\mathrm{2}}{\mathrm{4}^{\mathrm{1}} }\:+\:\frac{\mathrm{2}×\mathrm{3}}{\mathrm{4}^{\mathrm{2}} }\:+\:\frac{\mathrm{3}×\mathrm{4}}{\mathrm{4}^{\mathrm{3}} }\:+\:\frac{\mathrm{4}×\mathrm{5}}{\mathrm{4}^{\mathrm{4}} }\:+\:….. \\ $$
Answered by JDamian last updated on 21/Jul/20
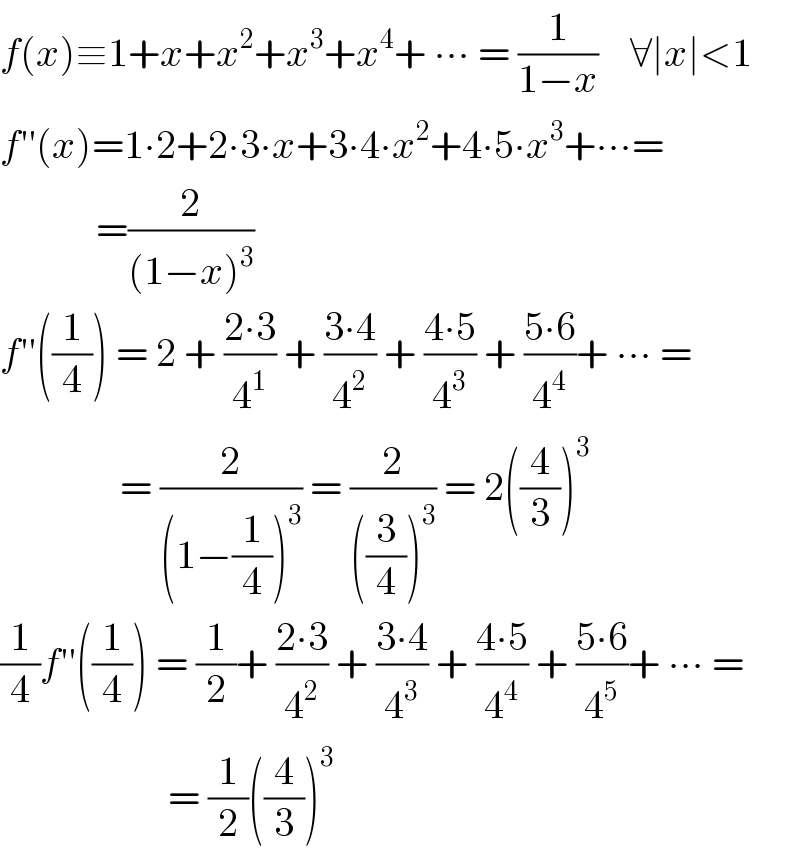
f(x)≡1+x+x^2 +x^3 +x^4 + ∙∙∙ = (1/(1−x)) ∀∣x∣<1 f′′(x)=1∙2+2∙3∙x+3∙4∙x^2 +4∙5∙x^3 +∙∙∙= =(2/((1−x)^3 )) f′′((1/4)) = 2 + ((2∙3)/4^1 ) + ((3∙4)/4^2 ) + ((4∙5)/4^3 ) + ((5∙6)/4^4 )+ ∙∙∙ = = (2/((1−(1/4))^3 )) = (2/(((3/4))^3 )) = 2((4/3))^3 (1/4)f′′((1/4)) = (1/2)+ ((2∙3)/4^2 ) + ((3∙4)/4^3 ) + ((4∙5)/4^4 ) + ((5∙6)/4^5 )+ ∙∙∙ = = (1/2)((4/3))^3
$${f}\left({x}\right)\equiv\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +\:\centerdot\centerdot\centerdot\:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:\:\:\forall\mid{x}\mid<\mathrm{1} \\ $$$${f}''\left({x}\right)=\mathrm{1}\centerdot\mathrm{2}+\mathrm{2}\centerdot\mathrm{3}\centerdot{x}+\mathrm{3}\centerdot\mathrm{4}\centerdot{x}^{\mathrm{2}} +\mathrm{4}\centerdot\mathrm{5}\centerdot{x}^{\mathrm{3}} +\centerdot\centerdot\centerdot= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$${f}''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:=\:\mathrm{2}\:+\:\frac{\mathrm{2}\centerdot\mathrm{3}}{\mathrm{4}^{\mathrm{1}} }\:+\:\frac{\mathrm{3}\centerdot\mathrm{4}}{\mathrm{4}^{\mathrm{2}} }\:+\:\frac{\mathrm{4}\centerdot\mathrm{5}}{\mathrm{4}^{\mathrm{3}} }\:+\:\frac{\mathrm{5}\centerdot\mathrm{6}}{\mathrm{4}^{\mathrm{4}} }+\:\centerdot\centerdot\centerdot\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{2}}{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{3}} }\:=\:\mathrm{2}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{f}''\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\:\frac{\mathrm{2}\centerdot\mathrm{3}}{\mathrm{4}^{\mathrm{2}} }\:+\:\frac{\mathrm{3}\centerdot\mathrm{4}}{\mathrm{4}^{\mathrm{3}} }\:+\:\frac{\mathrm{4}\centerdot\mathrm{5}}{\mathrm{4}^{\mathrm{4}} }\:+\:\frac{\mathrm{5}\centerdot\mathrm{6}}{\mathrm{4}^{\mathrm{5}} }+\:\centerdot\centerdot\centerdot\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$
Commented by Don08q last updated on 22/Jul/20
Thank you very much Sir
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *