Menu Close

Evaluate-1-2-x-4-x-dx-2-x-2-x-4-dx-3-x-2-x-4-dx-4-dx-2sinx-3secx-

Tinku Tara 0 Comments
Pin




Question Number 53119 by rahul 19 last updated on 18/Jan/19
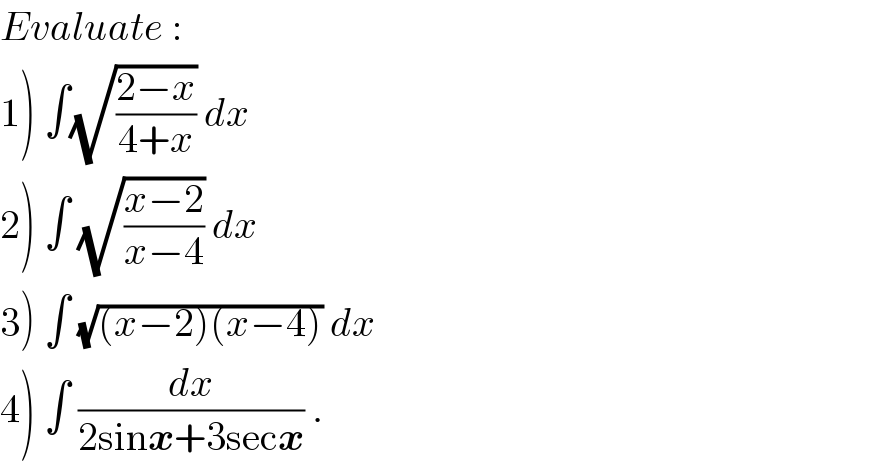
Evaluate : 1) ∫(√((2−x)/(4+x))) dx 2) ∫ (√((x−2)/(x−4))) dx 3) ∫ (√((x−2)(x−4))) dx 4) ∫ (dx/(2sinx+3secx)) .
$${Evaluate}\:: \\ $$$$\left.\mathrm{1}\right)\:\int\sqrt{\frac{\mathrm{2}−{x}}{\mathrm{4}+{x}}}\:{dx} \\ $$$$\left.\mathrm{2}\right)\:\int\:\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}\:{dx} \\ $$$$\left.\mathrm{3}\right)\:\int\:\sqrt{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{4}\right)}\:{dx} \\ $$$$\left.\mathrm{4}\right)\:\int\:\frac{{dx}}{\mathrm{2sin}\boldsymbol{{x}}+\mathrm{3sec}\boldsymbol{{x}}}\:. \\ $$
Commented by maxmathsup by imad last updated on 18/Jan/19
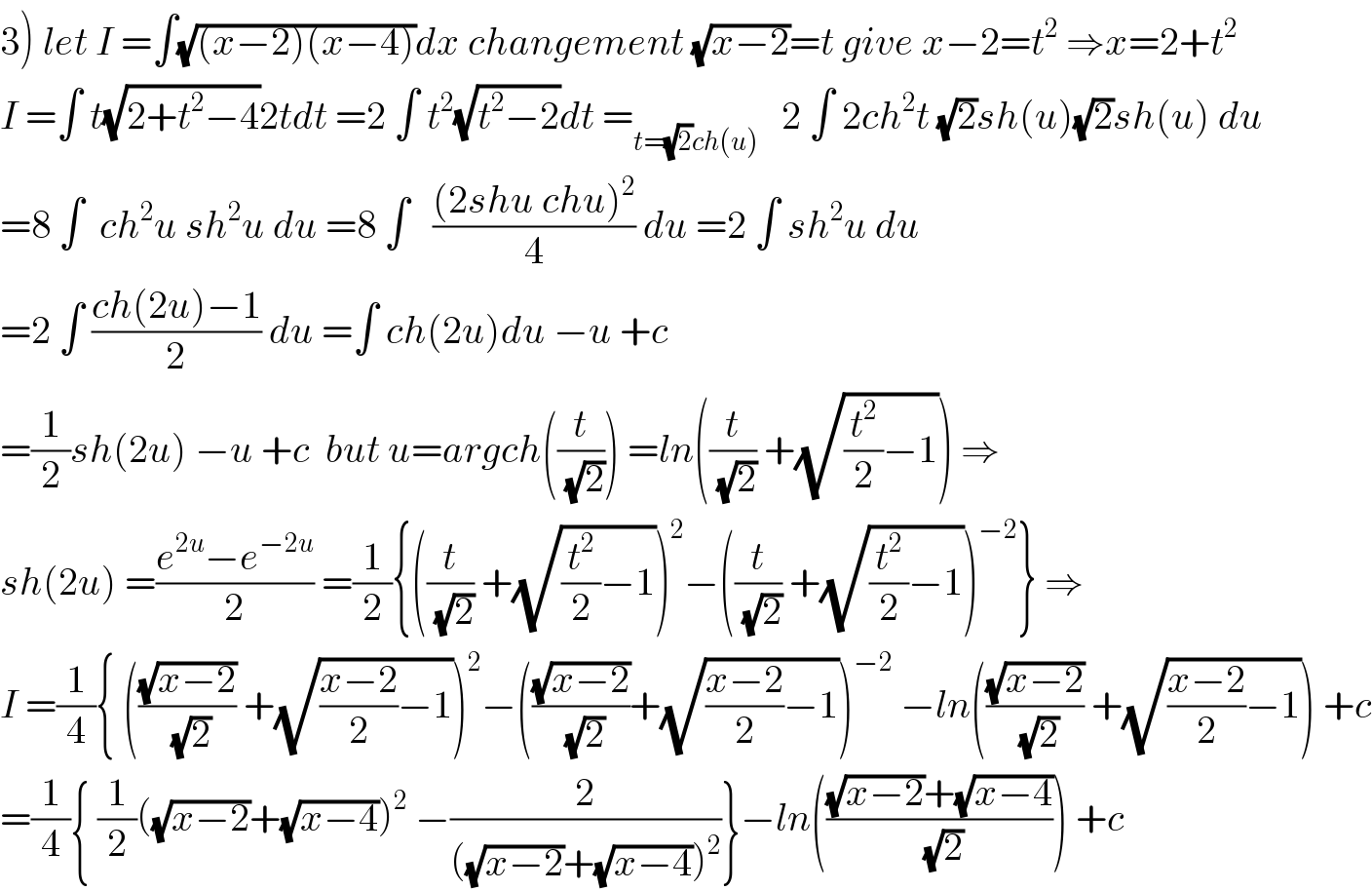
3) let I =∫(√((x−2)(x−4)))dx changement (√(x−2))=t give x−2=t^2 ⇒x=2+t^2 I =∫ t(√(2+t^2 −4))2tdt =2 ∫ t^2 (√(t^2 −2))dt =_(t=(√2)ch(u)) 2 ∫ 2ch^2 t (√2)sh(u)(√2)sh(u) du =8 ∫ ch^2 u sh^2 u du =8 ∫ (((2shu chu)^2 )/4) du =2 ∫ sh^2 u du =2 ∫ ((ch(2u)−1)/2) du =∫ ch(2u)du −u +c =(1/2)sh(2u) −u +c but u=argch((t/( (√2)))) =ln((t/( (√2))) +(√((t^2 /2)−1))) ⇒ sh(2u) =((e^(2u) −e^(−2u) )/2) =(1/2){((t/( (√2))) +(√((t^2 /2)−1)))^2 −((t/( (√2))) +(√((t^2 /2)−1)))^(−2) } ⇒ I =(1/4){ (((√(x−2))/( (√2))) +(√(((x−2)/2)−1)))^2 −(((√(x−2))/( (√2)))+(√(((x−2)/2)−1)))^(−2) −ln(((√(x−2))/( (√2))) +(√(((x−2)/2)−1))) +c =(1/4){ (1/2)((√(x−2))+(√(x−4)))^2 −(2/(((√(x−2))+(√(x−4)))^2 ))}−ln((((√(x−2))+(√(x−4)))/( (√2)))) +c
$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\int\sqrt{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{4}\right)}{dx}\:{changement}\:\sqrt{{x}−\mathrm{2}}={t}\:{give}\:{x}−\mathrm{2}={t}^{\mathrm{2}} \:\Rightarrow{x}=\mathrm{2}+{t}^{\mathrm{2}} \\ $$$${I}\:=\int\:{t}\sqrt{\mathrm{2}+{t}^{\mathrm{2}} −\mathrm{4}}\mathrm{2}{tdt}\:=\mathrm{2}\:\int\:{t}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} −\mathrm{2}}{dt}\:=_{{t}=\sqrt{\mathrm{2}}{ch}\left({u}\right)} \:\:\:\mathrm{2}\:\int\:\mathrm{2}{ch}^{\mathrm{2}} {t}\:\sqrt{\mathrm{2}}{sh}\left({u}\right)\sqrt{\mathrm{2}}{sh}\left({u}\right)\:{du} \\ $$$$=\mathrm{8}\:\int\:\:{ch}^{\mathrm{2}} {u}\:{sh}^{\mathrm{2}} {u}\:{du}\:=\mathrm{8}\:\int\:\:\:\frac{\left(\mathrm{2}{shu}\:{chu}\right)^{\mathrm{2}} }{\mathrm{4}}\:{du}\:=\mathrm{2}\:\int\:{sh}^{\mathrm{2}} {u}\:{du} \\ $$$$=\mathrm{2}\:\int\:\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}\:{du}\:=\int\:{ch}\left(\mathrm{2}{u}\right){du}\:−{u}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}{u}\right)\:−{u}\:+{c}\:\:{but}\:{u}={argch}\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\right)\:={ln}\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)\:\Rightarrow \\ $$$${sh}\left(\mathrm{2}{u}\right)\:=\frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} }{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{2}} −\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)^{−\mathrm{2}} \right\}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\left(\frac{\sqrt{{x}−\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\frac{{x}−\mathrm{2}}{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{{x}−\mathrm{2}}}{\:\sqrt{\mathrm{2}}}+\sqrt{\frac{{x}−\mathrm{2}}{\mathrm{2}}−\mathrm{1}}\right)^{−\mathrm{2}} \:−{ln}\left(\frac{\sqrt{{x}−\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\frac{{x}−\mathrm{2}}{\mathrm{2}}−\mathrm{1}}\right)\:+{c}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{x}−\mathrm{2}}+\sqrt{{x}−\mathrm{4}}\right)^{\mathrm{2}} \:−\frac{\mathrm{2}}{\left(\sqrt{{x}−\mathrm{2}}+\sqrt{{x}−\mathrm{4}}\right)^{\mathrm{2}} }\right\}−{ln}\left(\frac{\sqrt{{x}−\mathrm{2}}+\sqrt{{x}−\mathrm{4}}}{\:\sqrt{\mathrm{2}}}\right)\:+{c} \\ $$
Commented by Tawa1 last updated on 18/Jan/19
Sir please check your solution to my question 52841. i asked for some clarification sir. Thanks sir
$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{check}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{my}\:\mathrm{question}\:\:\mathrm{52841}. \\ $$$$\mathrm{i}\:\mathrm{asked}\:\mathrm{for}\:\mathrm{some}\:\mathrm{clarification}\:\mathrm{sir}.\:\:\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 23/Jan/19
2) let I =∫(√((x−2)/(x−4)))dx changement (√((x−2)/(x−4)))=t give ((x−2)/(x−4)) =t^2 ⇒ x−2 =t^2 x−4t^2 ⇒(1−t^2 )x =2−4t^2 ⇒x =((−4t^2 +2)/(1−t^2 )) =((4t^2 −2)/(t^2 −1)) ⇒ (dx/dt)=((8t(t^2 −1)−(4t^2 −2)2t)/((t^2 −1)^2 )) =((8t^3 −8t −8t^3 +4t)/((t^2 −1)^2 )) =((−4t)/((t^2 −1)^2 )) ⇒ I = ∫ t(((−4t)/((t^2 −1)^2 )))dt =−4 ∫ (t^2 /((t^2 −1)^2 ))dt =−4∫((t^2 −1 +1)/((t^2 −1)^2 ))dt =−4 ∫ (dt/(t^2 −1)) −4 ∫ (dt/((t^2 −1)^2 )) but ∫ (dt/(t^2 −1)) =(1/2)∫ ((1/(t−1)) −(1/(t+1)))dt =(1/2)ln∣((t−1)/(t+1))∣ +c_1 let decompose F(t)=(1/((t^2 −1)^2 )) ⇒F(t)=(1/((t−1)^2 (t+1)^2 )) =(a/(t−1)) +(b/((t−1)^2 )) +(c/((t+1))) +(d/((t+1)^2 )) b =lim_(t→1) (t−1)^2 F(t) =(1/4) d =lim_(t→−1) (t+1)^2 F(t) =(1/4) ⇒F(t)=(a/(t−1)) +(1/(4(t−1)^2 )) +(c/(t+1)) +(1/(4(t+1)^2 )) F(−t)=F(t) ⇒((−a)/(t+1)) +(1/(4(t+1)^2 )) + ((−c)/(t−1)) +(1/(4(t−1)^2 )) =F(t) ⇒c=−a ⇒ F(t) =(a/(t−1)) +(1/(4(t−1)^2 )) −(a/(t+1)) +(1/(4(t+1)^2 )) F(0)=1 =−a +(1/4) −a +(1/4) ⇒−2a+(1/2) =1 ⇒−2a =(1/2) ⇒a =−(1/4) ⇒ F(x)=−(1/(4(t−1))) +(1/(4(t+1))) +(1/(4(t−1)^2 )) +(1/(4(t+1)^2 )) ⇒ ∫ (dt/((t^2 −1)^2 )) =(1/4)ln∣((t+1)/(t−1))∣−(1/(4(t−1))) −(1/(4(t+1))) +c_2 ⇒ I =−2ln∣((t−1)/(t+1))∣ −ln∣((t+1)/(t−1))∣ +(1/(t−1)) +(1/(t+1)) +C ⇒ I =ln∣((t+1)/(t−1))∣ +(1/(t−1)) +(1/(t+1)) +C I =ln∣(((√((x−2)/(x−4)))+1)/( (√((x−2)/(x−4)))−1))∣ +(1/( (√((x−2)/(x−4)))−1)) +(1/( (√((x−2)/(x−4)))+1)) +C .
$$\left.\mathrm{2}\right)\:{let}\:{I}\:=\int\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}{dx}\:\:\:{changement}\:\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}={t}\:{give}\:\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}−\mathrm{2}\:={t}^{\mathrm{2}} {x}−\mathrm{4}{t}^{\mathrm{2}} \:\Rightarrow\left(\mathrm{1}−{t}^{\mathrm{2}} \right){x}\:=\mathrm{2}−\mathrm{4}{t}^{\mathrm{2}} \:\Rightarrow{x}\:=\frac{−\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{2}}{\mathrm{1}−{t}^{\mathrm{2}} }\:=\frac{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}}{{t}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}=\frac{\mathrm{8}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)−\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}\right)\mathrm{2}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{8}{t}^{\mathrm{3}} −\mathrm{8}{t}\:−\mathrm{8}{t}^{\mathrm{3}} \:+\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\:\int\:\:{t}\left(\frac{−\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\right){dt}\:=−\mathrm{4}\:\int\:\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} \:−\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=−\mathrm{4}\int\frac{{t}^{\mathrm{2}} −\mathrm{1}\:+\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=−\mathrm{4}\:\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}\:−\mathrm{4}\:\int\:\:\:\frac{{dt}}{\left({t}^{\mathrm{2}} \:−\mathrm{1}\right)^{\mathrm{2}} }\:{but} \\ $$$$\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:−\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}}{{t}−\mathrm{1}}\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:+{c}_{\mathrm{1}} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{{b}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{c}}{\left({t}+\mathrm{1}\right)}\:+\frac{{d}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${b}\:={lim}_{{t}\rightarrow\mathrm{1}} \left({t}−\mathrm{1}\right)^{\mathrm{2}} \:{F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${d}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right)^{\mathrm{2}} \:{F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{F}\left({t}\right)=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{c}}{{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(−{t}\right)={F}\left({t}\right)\:\Rightarrow\frac{−{a}}{{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+\:\frac{−{c}}{{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:={F}\left({t}\right)\:\Rightarrow{c}=−{a}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{{a}}{{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{1}\:=−{a}\:+\frac{\mathrm{1}}{\mathrm{4}}\:−{a}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow−\mathrm{2}{a}+\frac{\mathrm{1}}{\mathrm{2}}\:=\mathrm{1}\:\Rightarrow−\mathrm{2}{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{a}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{4}\left({t}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\mid−\frac{\mathrm{1}}{\mathrm{4}\left({t}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{4}\left({t}+\mathrm{1}\right)}\:+{c}_{\mathrm{2}} \:\:\Rightarrow \\ $$$${I}\:=−\mathrm{2}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:\:−{ln}\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\mid\:+\frac{\mathrm{1}}{{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{{t}+\mathrm{1}}\:+{C}\:\Rightarrow \\ $$$${I}\:={ln}\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\mid\:+\frac{\mathrm{1}}{{t}−\mathrm{1}}\:+\frac{\mathrm{1}}{{t}+\mathrm{1}}\:+{C} \\ $$$${I}\:={ln}\mid\frac{\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}+\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}−\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}−\mathrm{1}}\:+\frac{\mathrm{1}}{\:\sqrt{\frac{{x}−\mathrm{2}}{{x}−\mathrm{4}}}+\mathrm{1}}\:+{C}\:. \\ $$
Answered by MJS last updated on 18/Jan/19
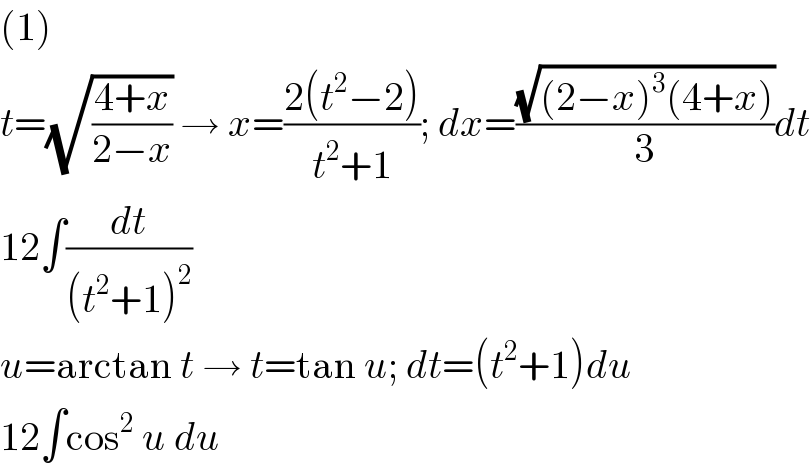
(1) t=(√((4+x)/(2−x))) → x=((2(t^2 −2))/(t^2 +1)); dx=((√((2−x)^3 (4+x)))/3)dt 12∫(dt/((t^2 +1)^2 )) u=arctan t → t=tan u; dt=(t^2 +1)du 12∫cos^2 u du
$$\left(\mathrm{1}\right) \\ $$$${t}=\sqrt{\frac{\mathrm{4}+{x}}{\mathrm{2}−{x}}}\:\rightarrow\:{x}=\frac{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{2}\right)}{{t}^{\mathrm{2}} +\mathrm{1}};\:{dx}=\frac{\sqrt{\left(\mathrm{2}−{x}\right)^{\mathrm{3}} \left(\mathrm{4}+{x}\right)}}{\mathrm{3}}{dt} \\ $$$$\mathrm{12}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${u}=\mathrm{arctan}\:{t}\:\rightarrow\:{t}=\mathrm{tan}\:{u};\:{dt}=\left({t}^{\mathrm{2}} +\mathrm{1}\right){du} \\ $$$$\mathrm{12}\int\mathrm{cos}^{\mathrm{2}} \:{u}\:{du} \\ $$
Answered by MJS last updated on 18/Jan/19
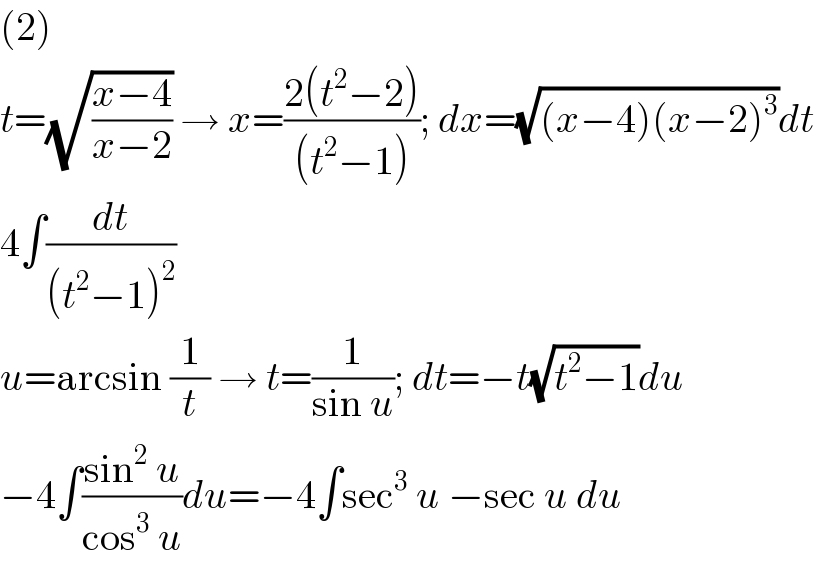
(2) t=(√((x−4)/(x−2))) → x=((2(t^2 −2))/((t^2 −1))); dx=(√((x−4)(x−2)^3 ))dt 4∫(dt/((t^2 −1)^2 )) u=arcsin (1/t) → t=(1/(sin u)); dt=−t(√(t^2 −1))du −4∫((sin^2 u)/(cos^3 u))du=−4∫sec^3 u −sec u du
$$\left(\mathrm{2}\right) \\ $$$${t}=\sqrt{\frac{{x}−\mathrm{4}}{{x}−\mathrm{2}}}\:\rightarrow\:{x}=\frac{\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{2}\right)}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)};\:{dx}=\sqrt{\left({x}−\mathrm{4}\right)\left({x}−\mathrm{2}\right)^{\mathrm{3}} }{dt} \\ $$$$\mathrm{4}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${u}=\mathrm{arcsin}\:\frac{\mathrm{1}}{{t}}\:\rightarrow\:{t}=\frac{\mathrm{1}}{\mathrm{sin}\:{u}};\:{dt}=−{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$$−\mathrm{4}\int\frac{\mathrm{sin}^{\mathrm{2}} \:{u}}{\mathrm{cos}^{\mathrm{3}} \:{u}}{du}=−\mathrm{4}\int\mathrm{sec}^{\mathrm{3}} \:{u}\:−\mathrm{sec}\:{u}\:{du} \\ $$
Answered by MJS last updated on 18/Jan/19
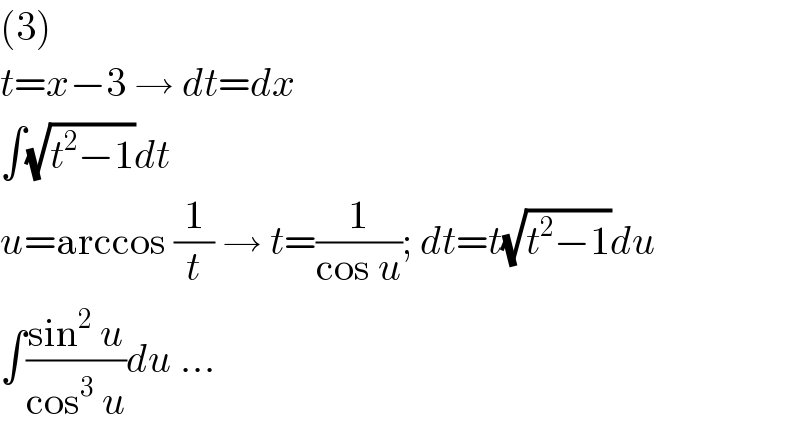
(3) t=x−3 → dt=dx ∫(√(t^2 −1))dt u=arccos (1/t) → t=(1/(cos u)); dt=t(√(t^2 −1))du ∫((sin^2 u)/(cos^3 u))du ...
$$\left(\mathrm{3}\right) \\ $$$${t}={x}−\mathrm{3}\:\rightarrow\:{dt}={dx} \\ $$$$\int\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$${u}=\mathrm{arccos}\:\frac{\mathrm{1}}{{t}}\:\rightarrow\:{t}=\frac{\mathrm{1}}{\mathrm{cos}\:{u}};\:{dt}={t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{u}}{\mathrm{cos}^{\mathrm{3}} \:{u}}{du}\:… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19
1)∫((2−x)/( (√((4+x)(2−x)))))dx ∫((2−x)/( (√(8−4x+2x−x^2 ))))dx ∫((2−x)/( (√(8−2x−x^2 )))) (1/2)∫((−2−2x+6)/( (√(8−2x−x^2 ))))dx =(1/2)∫((d(8−2x−x^2 ))/( (√(8−2x−x^2 ))))+3∫(dx/( (√((3)^2 −(x+1)^2 )))) =(1/2)×(((8−2x−x^2 )^(((−1)/2)+1) )/(((−1)/2)+1))+3sin^(−1) (((x+1)/3))+c =(8−2x−x^2 )^(1/2) +3sin^(−1) (((x+1)/3))+c 2)∫((x−2)/( (√((x−2)(x−4)))))dx ∫((x−2)/( (√(x^2 −6x+8))))dx (1/2)∫((2x−6+2)/( (√(x^2 −6x+8))))dx (1/2)∫((d(x^2 −6x+8))/( (√(x^2 −6x+8))))+∫(dx/( (√((x−3)^2 −1)))) (1/2)×(((x^2 −6x+8)^(((−1)/2)+1) )/(((−1)/2)+1))+ln{(x−3)+(√((x−3)^2 −1)) }+c =(x^2 −6x+8)^(1/2) +ln{(x−3)+(√(x^2 −6x+8)) }+c 3∫(√((x−2)(x−4))) dx ∫(√((x−3)^2 −1)) dx =(((x−3))/2)(√((x−3)^2 −1)) −(1/2)ln{(x−3)+(√((x−3)^2 −1)) }+c =(((x−3))/2)(√(x^2 −6x+8)) −(1/2)ln{(x−3)+(√((x^2 −6x+8))
$$\left.\mathrm{1}\right)\int\frac{\mathrm{2}−{x}}{\:\sqrt{\left(\mathrm{4}+{x}\right)\left(\mathrm{2}−{x}\right)}}{dx} \\ $$$$\int\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{8}−\mathrm{4}{x}+\mathrm{2}{x}−{x}^{\mathrm{2}} }}{dx} \\ $$$$\int\frac{\mathrm{2}−{x}}{\:\sqrt{\mathrm{8}−\mathrm{2}{x}−{x}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}−\mathrm{2}{x}+\mathrm{6}}{\:\sqrt{\mathrm{8}−\mathrm{2}{x}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{8}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{8}−\mathrm{2}{x}−{x}^{\mathrm{2}} }}+\mathrm{3}\int\frac{{dx}}{\:\sqrt{\left(\mathrm{3}\right)^{\mathrm{2}} −\left({x}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left(\mathrm{8}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}+\mathrm{3}{sin}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)+{c} \\ $$$$=\left(\mathrm{8}−\mathrm{2}{x}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{3}{sin}^{−\mathrm{1}} \left(\frac{{x}+\mathrm{1}}{\mathrm{3}}\right)+{c} \\ $$$$\left.\mathrm{2}\right)\int\frac{{x}−\mathrm{2}}{\:\sqrt{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{4}\right)}}{dx} \\ $$$$\int\frac{{x}−\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{6}+\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}\right)}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}}}+\int\frac{{dx}}{\:\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} }{\frac{−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}+{ln}\left\{\left({x}−\mathrm{3}\right)+\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{1}}\:\right\}+{c} \\ $$$$=\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +{ln}\left\{\left({x}−\mathrm{3}\right)+\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}}\:\right\}+{c} \\ $$$$\mathrm{3}\int\sqrt{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{4}\right)}\:{dx} \\ $$$$\int\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{1}}\:{dx} \\ $$$$=\frac{\left({x}−\mathrm{3}\right)}{\mathrm{2}}\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left({x}−\mathrm{3}\right)+\sqrt{\left({x}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{1}}\:\right\}+{c} \\ $$$$=\frac{\left({x}−\mathrm{3}\right)}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left\{\left({x}−\mathrm{3}\right)+\sqrt{\left({x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{8}\right.}\right. \\ $$$$ \\ $$
Commented by rahul 19 last updated on 18/Jan/19
Thank you Sir!
$${Thank}\:{you}\:{Sir}! \\ $$
Commented by Otchere Abdullai last updated on 18/Jan/19
wow! well done sir!
$${wow}!\:{well}\:{done}\:{sir}! \\ $$
Answered by MJS last updated on 18/Jan/19
(4) =∫((cos x)/(3+cos x sin x))dx Weyerstrass t=tan (x/2) → x=2arctan t; dx=2cos^2 (x/2) dt=((2dt)/(t^2 +1)) cos x =−((t^2 −1)/(t^2 +1)); sin x =((2t)/(t^2 +1)) −2∫((t^2 −1)/((t^2 −2t+3)(3t^2 +2t+1)))dt now decompose... ((t^2 −1)/((t^2 −2t+3)(3t^2 +2t+1)))=(1/8)×((t+1)/(t^2 −2t+3))−(3/8)×((t+1)/(3t^2 +2t+1)) ((t+1)/(t^2 −2t+3))=((t−1)/(t^2 −2t+3))+(2/(t^2 −2t+3)) ((t+1)/(3t^2 +2t+1))=((6t+2)/(6(3t^2 +2t+1)))+(4/(6(3t^2 +2t+1)))= =(1/3)×((3t+1)/(3t^2 +2t+1))+(2/3)×(1/(3t^2 +2t+1)) now use formulas
$$\left(\mathrm{4}\right) \\ $$$$=\int\frac{\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{cos}\:{x}\:\mathrm{sin}\:{x}}{dx} \\ $$$$\mathrm{Weyerstrass} \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{x}=\mathrm{2arctan}\:{t};\:{dx}=\mathrm{2cos}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\:{dt}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{cos}\:{x}\:=−\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}};\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$−\mathrm{2}\int\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}\right)\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{dt} \\ $$$$\mathrm{now}\:\mathrm{decompose}… \\ $$$$\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}\right)\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{8}}×\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{8}}×\frac{{t}+\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}} \\ $$$$\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}}=\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}}+\frac{\mathrm{2}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{3}} \\ $$$$\frac{{t}+\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}=\frac{\mathrm{6}{t}+\mathrm{2}}{\mathrm{6}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{6}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}{t}+\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{formulas} \\ $$
Commented by rahul 19 last updated on 18/Jan/19
Thank You Sir!
$${Thank}\:{You}\:{Sir}! \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Jan/19
4)∫(dx/(2sinx+3secx)) ∫((cosxdx)/(3+2sinxcosx)) (1/2)∫((cosx−sinx+cosx+sinx)/(3+2sinxcosx))dx (1/2)∫((cosx−sinx)/(2+(sinx+cosx)^2 ))dx+(1/2)∫((d(sinx−cosx))/(4−(1−2sinxcosx))) (1/2)∫((d(sinx+cosx))/(((√2) )^2 +(sinx+cosx)^2 ))+(1/2)∫((d(sinx−cosx))/(4−(sinx−cosx)^2 ))←formula∫(dx/(a^2 −x^2 )) (1/2)×(1/( (√2)))tan^(−1) (((sinx+cosx)/( (√2))))+(1/2)×(1/(2×2))ln(((2+sinx−cosx)/(2−sinx+cosx)))+c
$$\left.\mathrm{4}\right)\int\frac{{dx}}{\mathrm{2}{sinx}+\mathrm{3}{secx}} \\ $$$$\int\frac{{cosxdx}}{\mathrm{3}+\mathrm{2}{sinxcosx}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cosx}−{sinx}+{cosx}+{sinx}}{\mathrm{3}+\mathrm{2}{sinxcosx}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cosx}−{sinx}}{\mathrm{2}+\left({sinx}+{cosx}\right)^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{4}−\left(\mathrm{1}−\mathrm{2}{sinxcosx}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({sinx}+{cosx}\right)}{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +\left({sinx}+{cosx}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{4}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }\leftarrow{formula}\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{sinx}+{cosx}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}×\mathrm{2}}{ln}\left(\frac{\mathrm{2}+{sinx}−{cosx}}{\mathrm{2}−{sinx}+{cosx}}\right)+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *