Question Number 83807 by niroj last updated on 06/Mar/20

$$\:\:\boldsymbol{\mathrm{Evaluate}}: \\ $$$$\:\:\int\:\:\frac{\:\mathrm{1}}{\boldsymbol{\mathrm{ax}}^{\mathrm{2}} +\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{c}}}\boldsymbol{\mathrm{dx}} \\ $$
Commented by mathmax by abdo last updated on 06/Mar/20

$${I}\:=\int\:\:\frac{{dx}}{{ax}^{\mathrm{2}} \:+{bx}\:+{c}} \\ $$$${case}\:\mathrm{1}\:\:{a}=\mathrm{0}\:{and}\:{b}\neq\mathrm{0}\:\Rightarrow{I}\:=\frac{\mathrm{1}}{{b}}{ln}\mid{bx}+{c}\mid\:+{K}\:{now}\:{we}\:{take}\:{a}\neq\mathrm{0} \\ $$$$\Delta\:={b}^{\mathrm{2}} −\mathrm{4}{ac}\:\:\:{case}\:\mathrm{1}\:\:\Delta>\mathrm{0}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−{b}+\sqrt{{b}^{\mathrm{2}} −{ac}}}{\mathrm{2}{a}}\:\:{and}\:{x}_{\mathrm{2}} =\frac{−{b}−\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$${I}\:=\int\:\:\frac{{dx}}{{a}\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{{a}}\int\:\left(\frac{\mathrm{1}}{{x}−{x}_{\mathrm{1}} }−\frac{\mathrm{1}}{{x}−{x}_{\mathrm{2}} }\right){dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{ln}\mid\frac{{x}−{x}_{\mathrm{1}} }{{x}−{x}_{\mathrm{2}} }\mid\:+{C} \\ $$$${case}\mathrm{2}\:\:\Delta<\mathrm{0}\:\Rightarrow{b}^{\mathrm{2}} <\mathrm{4}{ac}\:\Rightarrow{I}\:=\int\:\:\frac{{dx}}{{a}\left(\:{x}^{\mathrm{2}} \:+\frac{{b}}{{a}}{x}\:+\frac{{c}}{{a}}\right)} \\ $$$$=\frac{\mathrm{1}}{{a}}\int\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{2}\frac{{b}}{\mathrm{2}{a}}{x}\:+\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\:+\frac{{c}}{{a}}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)} \\ $$$$=\frac{\mathrm{1}}{{a}}\:\int\:\:\:\frac{{dx}}{\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}\:\:=_{{x}+\frac{{b}}{\mathrm{2}{a}}=\sqrt{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}{z}} \frac{\mathrm{1}}{{a}}\int\:\:\frac{\mathrm{1}}{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}×\sqrt{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}\:{dz} \\ $$$$=\frac{\mathrm{4}{a}}{\mathrm{4}{ac}−{b}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}{\mathrm{2}\mid{a}\mid}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}}\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)\right)\:+{K} \\ $$$$=\frac{\mathrm{2}{a}}{\mid{a}\mid\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}}\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)\right)\:+{K} \\ $$$$= \\ $$$$ \\ $$
Answered by john santu last updated on 06/Mar/20
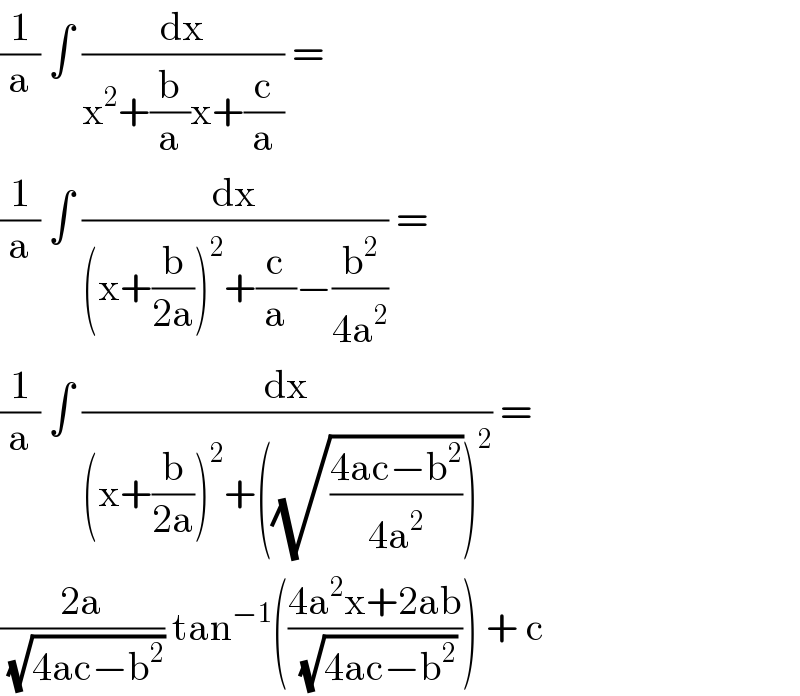
$$\frac{\mathrm{1}}{\mathrm{a}}\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{b}}{\mathrm{a}}\mathrm{x}+\frac{\mathrm{c}}{\mathrm{a}}}\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{b}}{\mathrm{2a}}\right)^{\mathrm{2}} +\frac{\mathrm{c}}{\mathrm{a}}−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{4a}^{\mathrm{2}} }}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{b}}{\mathrm{2a}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{4ac}−\mathrm{b}^{\mathrm{2}} }{\mathrm{4a}^{\mathrm{2}} }}\right)^{\mathrm{2}} }\:= \\ $$$$\frac{\mathrm{2a}}{\:\sqrt{\mathrm{4ac}−\mathrm{b}^{\mathrm{2}} }}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4a}^{\mathrm{2}} \mathrm{x}+\mathrm{2ab}}{\:\sqrt{\mathrm{4ac}−\mathrm{b}^{\mathrm{2}} }}\right)\:+\:\mathrm{c} \\ $$
Answered by TANMAY PANACEA last updated on 06/Mar/20

$${ax}^{\mathrm{2}} +{bx}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{a}}\left(\mathrm{4}{a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{4}{abx}+\mathrm{4}{ac}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{a}}\left\{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} +\mathrm{4}{ac}−{b}^{\mathrm{2}} \right\} \\ $$$${condition}…\left(\mathrm{1}\right) \\ $$$${when}\:{b}^{\mathrm{2}} >\mathrm{4}{ac} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{a}}\left\{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} −\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{a}}\left\{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} −\left(\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\:\right)^{\mathrm{2}} \right\} \\ $$$${so}\:\int\frac{{dx}}{{ax}^{\mathrm{2}} +{bx}+{c}} \\ $$$$\int\frac{{dx}}{\frac{\mathrm{1}}{\mathrm{4}{a}}\left\{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} −\left(\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\:\right)^{\mathrm{2}} \right.} \\ $$$${now}\:{pls}\:{use}\:{formula}\int\frac{{dy}}{{y}^{\mathrm{2}} −{k}^{\mathrm{2}} } \\ $$$${condition}\:\mathrm{2} \\ $$$${b}^{\mathrm{2}} <\mathrm{4}{ac} \\ $$$$\int\frac{{dx}}{\frac{\mathrm{1}}{\mathrm{4}{a}}\left\{\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\right)^{\mathrm{2}} \right.} \\ $$$${now}\:{use}\:{formula}\:\int\frac{{dy}}{{y}^{\mathrm{2}} +{k}^{\mathrm{2}} } \\ $$$${condition}\:\mathrm{3} \\ $$$${b}^{\mathrm{2}} =\mathrm{4}{ac} \\ $$$$\int\frac{{dx}}{\frac{\mathrm{1}}{\mathrm{4}{a}}\left(\mathrm{2}{ax}+{b}\right)^{\mathrm{2}} } \\ $$
Commented by niroj last updated on 06/Mar/20

$${thanks}\:{to}\:{all}. \\ $$
