Question Number 43551 by peter frank last updated on 11/Sep/18
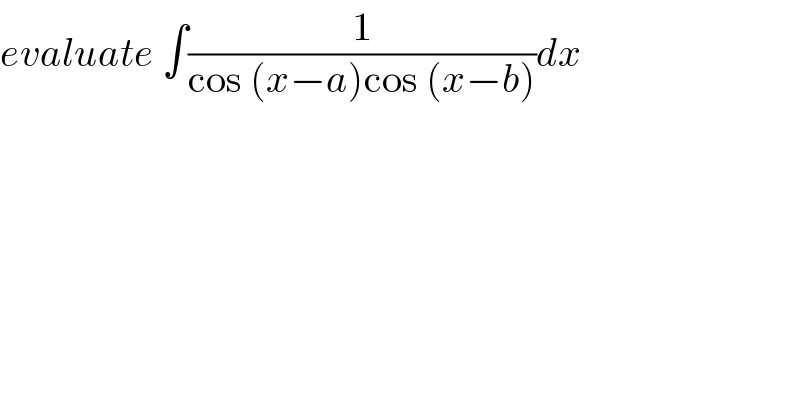
$${evaluate}\:\int\frac{\mathrm{1}}{\mathrm{cos}\:\left({x}−{a}\right)\mathrm{cos}\:\left({x}−{b}\right)}{dx} \\ $$
Answered by MJS last updated on 12/Sep/18
![∫(dx/(cos(x−a)cos(x−b)))= [t=x−a → dx=dt] =∫(dt/(cos t cos(t+a−b)))= [cos(α+β)=cos α cos β −sin α sin β] =∫(dt/(cos t (cos t cos(a−b)−sin t sin(a−b))))= [cos(a−b)=p; sin(a−b)=q] =∫(dt/(pcos^2 t +qcos t sin t))= =∫(dt/(cos^2 t (p+qtan t)))=∫((sec^2 t)/(p+qtan t))dt= [u=tan t → dt=(du/(sec^2 t))] =∫(du/(p+qu))= [v=p+qu → du=(dv/q)] =(1/q)∫(dv/v)=(1/q)ln v=(1/q)ln(p+qu)=(1/q)ln(p+qtan t)= =(1/(sin(a−b)))ln∣cos(a−b)+sin(a−b)tan(x−a)∣+C](https://www.tinkutara.com/question/Q43556.png)
$$\int\frac{{dx}}{\mathrm{cos}\left({x}−{a}\right)\mathrm{cos}\left({x}−{b}\right)}= \\ $$$$\:\:\:\:\:\left[{t}={x}−{a}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{cos}\:{t}\:\mathrm{cos}\left({t}+{a}−{b}\right)}= \\ $$$$\:\:\:\:\:\left[\mathrm{cos}\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\right] \\ $$$$=\int\frac{{dt}}{\mathrm{cos}\:{t}\:\left(\mathrm{cos}\:{t}\:\mathrm{cos}\left({a}−{b}\right)−\mathrm{sin}\:{t}\:\mathrm{sin}\left({a}−{b}\right)\right)}= \\ $$$$\:\:\:\:\:\left[\mathrm{cos}\left({a}−{b}\right)={p};\:\mathrm{sin}\left({a}−{b}\right)={q}\right] \\ $$$$=\int\frac{{dt}}{{p}\mathrm{cos}^{\mathrm{2}} \:{t}\:+{q}\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}}= \\ $$$$=\int\frac{{dt}}{\mathrm{cos}^{\mathrm{2}} \:{t}\:\left({p}+{q}\mathrm{tan}\:{t}\right)}=\int\frac{\mathrm{sec}^{\mathrm{2}} \:{t}}{{p}+{q}\mathrm{tan}\:{t}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{tan}\:{t}\:\rightarrow\:{dt}=\frac{{du}}{\mathrm{sec}^{\mathrm{2}} \:{t}}\right] \\ $$$$=\int\frac{{du}}{{p}+{qu}}= \\ $$$$\:\:\:\:\:\left[{v}={p}+{qu}\:\rightarrow\:{du}=\frac{{dv}}{{q}}\right] \\ $$$$=\frac{\mathrm{1}}{{q}}\int\frac{{dv}}{{v}}=\frac{\mathrm{1}}{{q}}\mathrm{ln}\:{v}=\frac{\mathrm{1}}{{q}}\mathrm{ln}\left({p}+{qu}\right)=\frac{\mathrm{1}}{{q}}\mathrm{ln}\left({p}+{q}\mathrm{tan}\:{t}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{sin}\left({a}−{b}\right)}\mathrm{ln}\mid\mathrm{cos}\left({a}−{b}\right)+\mathrm{sin}\left({a}−{b}\right)\mathrm{tan}\left({x}−{a}\right)\mid+{C} \\ $$
