Question Number 88236 by Rio Michael last updated on 09/Apr/20
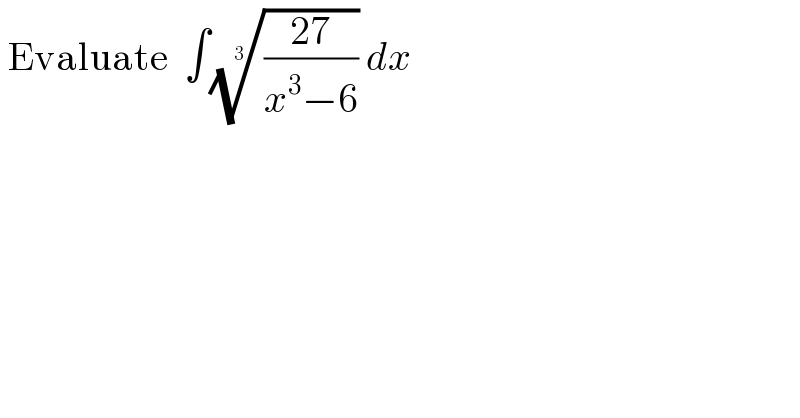
$$\:\mathrm{Evaluate}\:\:\int\sqrt[{\mathrm{3}}]{\frac{\mathrm{27}}{{x}^{\mathrm{3}} −\mathrm{6}}}\:{dx}\: \\ $$
Answered by MJS last updated on 09/Apr/20
![∫(((27)/(x^3 −6)))^(1/3) dx=3∫(dx/( ((x^3 −6))^(1/3) ))= [t=(x/( ((x^3 −6))^(1/3) )) → dx=−(((x^3 −6)^(4/3) )/6)dt] =−3∫(dt/(t^3 −1))=∫((t+2)/(t^2 +t+1))dt−∫(dt/(t−1))= =(√3)arctan ((2t+1)/( (√3))) +(1/2)ln (t^2 +t+1) −ln (t−1) = =(√3)arctan ((2t+1)/( (√3))) +(1/2)ln ((t^2 +t+1)/((t−1)^2 )) now insert t=(x/( ((x^3 −6))^(1/3) ))](https://www.tinkutara.com/question/Q88244.png)
$$\int\sqrt[{\mathrm{3}}]{\frac{\mathrm{27}}{{x}^{\mathrm{3}} −\mathrm{6}}}{dx}=\mathrm{3}\int\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{6}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{6}}}\:\rightarrow\:{dx}=−\frac{\left({x}^{\mathrm{3}} −\mathrm{6}\right)^{\mathrm{4}/\mathrm{3}} }{\mathrm{6}}{dt}\right] \\ $$$$=−\mathrm{3}\int\frac{{dt}}{{t}^{\mathrm{3}} −\mathrm{1}}=\int\frac{{t}+\mathrm{2}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}−\int\frac{{dt}}{{t}−\mathrm{1}}= \\ $$$$=\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:−\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:= \\ $$$$=\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{now}\:\mathrm{insert}\:{t}=\frac{{x}}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} −\mathrm{6}}} \\ $$
Commented by Rio Michael last updated on 09/Apr/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 09/Apr/20
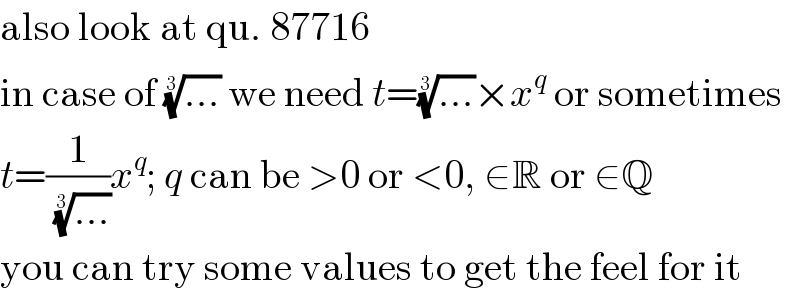
$$\mathrm{also}\:\mathrm{look}\:\mathrm{at}\:\mathrm{qu}.\:\mathrm{87716} \\ $$$$\mathrm{in}\:\mathrm{case}\:\mathrm{of}\:\sqrt[{\mathrm{3}}]{…}\:\mathrm{we}\:\mathrm{need}\:{t}=\sqrt[{\mathrm{3}}]{…}×{x}^{{q}} \:\mathrm{or}\:\mathrm{sometimes} \\ $$$${t}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{…}}{x}^{{q}} ;\:{q}\:\mathrm{can}\:\mathrm{be}\:>\mathrm{0}\:\mathrm{or}\:<\mathrm{0},\:\in\mathbb{R}\:\mathrm{or}\:\in\mathbb{Q} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{try}\:\mathrm{some}\:\mathrm{values}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{feel}\:\mathrm{for}\:\mathrm{it} \\ $$
Commented by Rio Michael last updated on 09/Apr/20
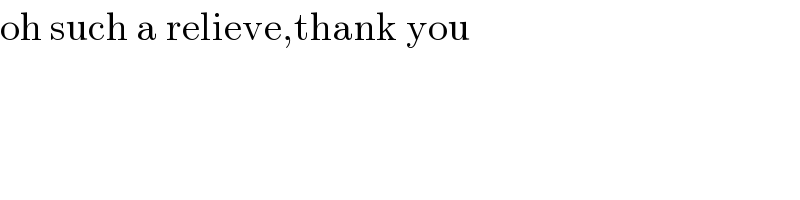
$$\mathrm{oh}\:\mathrm{such}\:\mathrm{a}\:\mathrm{relieve},\mathrm{thank}\:\mathrm{you} \\ $$
