Question Number 97136 by I want to learn more last updated on 06/Jun/20
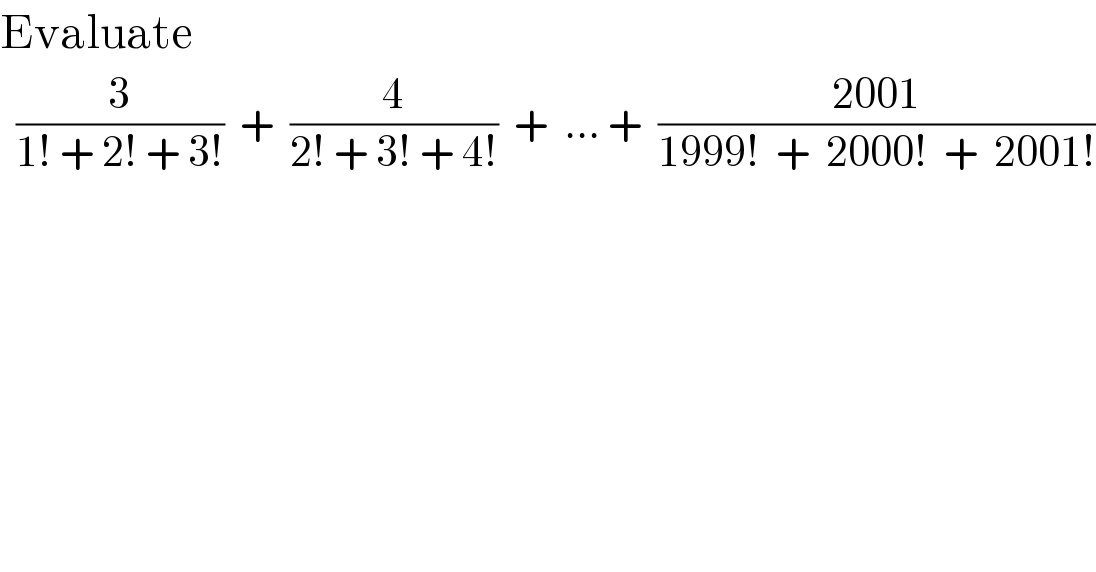
$$\mathrm{Evaluate} \\ $$$$\:\:\frac{\mathrm{3}}{\mathrm{1}!\:+\:\mathrm{2}!\:+\:\mathrm{3}!}\:\:+\:\:\frac{\mathrm{4}}{\mathrm{2}!\:+\:\mathrm{3}!\:+\:\mathrm{4}!}\:\:+\:\:…\:+\:\:\frac{\mathrm{2001}}{\mathrm{1999}!\:\:+\:\:\mathrm{2000}!\:\:+\:\:\mathrm{2001}!} \\ $$
Commented by 06122004 last updated on 06/Jun/20

$$\ast{Yechim}\ast \\ $$$${n}!+\left({n}+\mathrm{1}\right)!+\left({n}+\mathrm{2}\right)!={n}!\left(\mathrm{1}+\left({n}+\mathrm{1}\right)+\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\right)= \\ $$$$={n}!\ast\left({n}+\mathrm{2}\right)^{\mathrm{2}} \:\:\circledast \\ $$$$\frac{\mathrm{3}}{\mathrm{1}!\ast\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}!\ast\mathrm{4}^{\mathrm{2}} }+…+\frac{\mathrm{2001}}{\mathrm{1999}!\ast\mathrm{2001}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}!\ast\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}!\ast\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{1999}!\ast\mathrm{2001}}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+…+\frac{\mathrm{2000}}{\mathrm{2001}!}= \\ $$$$=\frac{\mathrm{3}−\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{4}−\mathrm{1}}{\mathrm{4}!}+…+\frac{\mathrm{2001}−\mathrm{1}}{\mathrm{2001}!}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}+…+\frac{\mathrm{1}}{\mathrm{2000}!}−\frac{\mathrm{1}}{\mathrm{2001}!}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{2001}!}=\frac{\frac{\mathrm{2001}!}{\mathrm{2}}−\mathrm{1}}{\mathrm{2001}!}=\frac{\mathrm{2001}!−\mathrm{2}}{\mathrm{2}\ast\mathrm{2001}!}\:\:\blacktriangle \\ $$$$\ast{Javob}\ast\:\frac{\mathrm{2001}!−\mathrm{2}}{\mathrm{2}\ast\mathrm{2001}!} \\ $$$${Abdullaxatov}\:{Jasurbek} \\ $$
Commented by I want to learn more last updated on 06/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by 06122004 last updated on 06/Jun/20

$${ok}! \\ $$
