Question Number 33155 by Joel578 last updated on 11/Apr/18
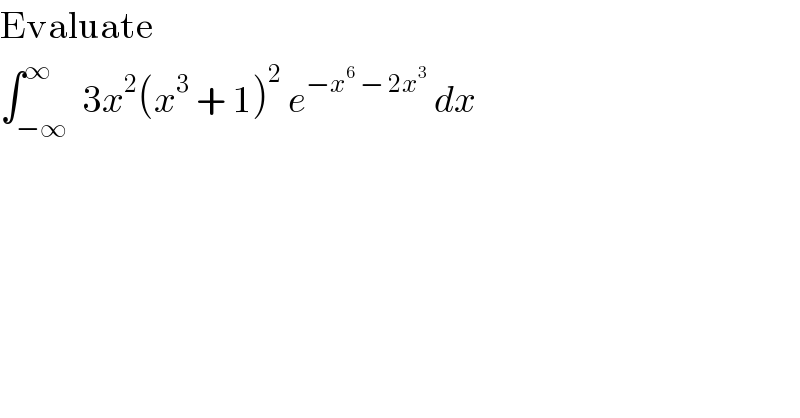
$$\mathrm{Evaluate} \\ $$$$\int_{−\infty} ^{\infty} \:\mathrm{3}{x}^{\mathrm{2}} \left({x}^{\mathrm{3}} \:+\:\mathrm{1}\right)^{\mathrm{2}} \:{e}^{−{x}^{\mathrm{6}} \:−\:\mathrm{2}{x}^{\mathrm{3}} } \:{dx} \\ $$
Commented by Joel578 last updated on 11/Apr/18
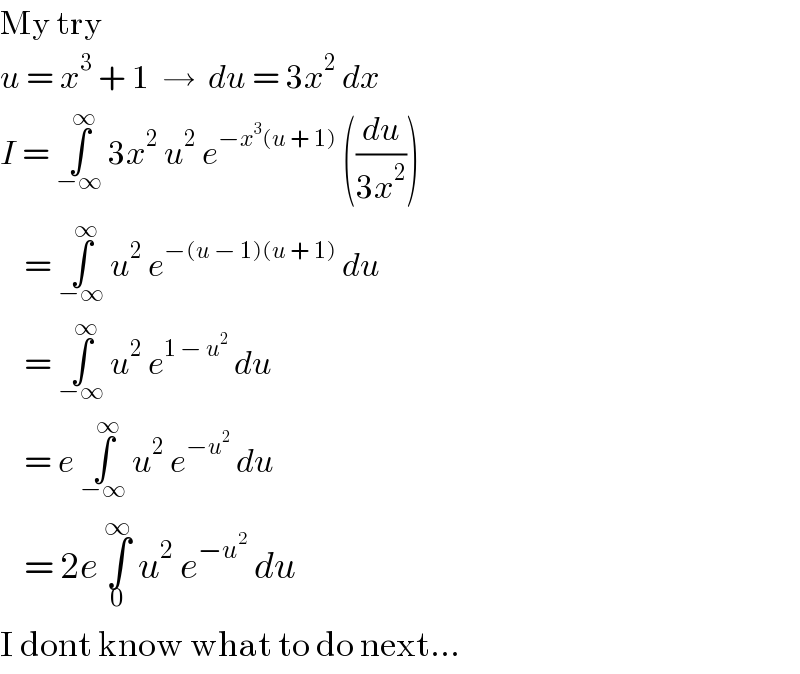
$$\mathrm{My}\:\mathrm{try} \\ $$$${u}\:=\:{x}^{\mathrm{3}} \:+\:\mathrm{1}\:\:\rightarrow\:\:{du}\:=\:\mathrm{3}{x}^{\mathrm{2}} \:{dx} \\ $$$${I}\:=\:\underset{−\infty} {\overset{\infty} {\int}}\:\mathrm{3}{x}^{\mathrm{2}} \:{u}^{\mathrm{2}} \:{e}^{−{x}^{\mathrm{3}} \left({u}\:+\:\mathrm{1}\right)} \:\left(\frac{{du}}{\mathrm{3}{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:=\:\underset{−\infty} {\overset{\infty} {\int}}\:{u}^{\mathrm{2}} \:{e}^{−\left({u}\:−\:\mathrm{1}\right)\left({u}\:+\:\mathrm{1}\right)} \:{du} \\ $$$$\:\:\:\:=\:\underset{−\infty} {\overset{\infty} {\int}}\:{u}^{\mathrm{2}} \:{e}^{\mathrm{1}\:−\:{u}^{\mathrm{2}} } \:{du} \\ $$$$\:\:\:\:=\:{e}\:\underset{−\infty} {\overset{\infty} {\int}}\:{u}^{\mathrm{2}} \:{e}^{−{u}^{\mathrm{2}} } \:{du} \\ $$$$\:\:\:\:=\:\mathrm{2}{e}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:{u}^{\mathrm{2}} \:{e}^{−{u}^{\mathrm{2}} } \:{du} \\ $$$$\mathrm{I}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{what}\:\mathrm{to}\:\mathrm{do}\:\mathrm{next}… \\ $$
Commented by prof Abdo imad last updated on 11/Apr/18
![let put I = ∫_(−∞) ^(+∞) 3x^2 (x^3 +1)^2 e^(−x^6 −2x^3 ) dx .ch.x^3 =t give I =∫_(−∞) ^(+∞) (t+1)^2 e^(−t^2 −2t) dt I =−(1/2) ∫_(−∞) ^(+∞) (t+1)(−2t−2)e^(−t^2 −2t) dt (by parts) −2I = [(t+1)e^(−t^2 −2t) ]_(−∞) ^(+∞) −∫_(−∞) ^(+∞) e^(−t^2 −2t) dt ⇒ 2I = ∫_(−∞) ^(+∞) e^(−( (t+1)^2 −1)) dt = e ∫_(−∞) ^(+∞) e^(−(t+1)^2 ) dt =_(t+1=x) e ∫_(−∞) ^(+∞) e^(−x^2 ) dx = e (√(π )) ⇒ I = ((e(√π))/2) brcause ∫_(−∞) ^(+∞) e^(−x^2 ) dx=(√π) .](https://www.tinkutara.com/question/Q33165.png)
$${let}\:{put}\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\mathrm{3}{x}^{\mathrm{2}} \left({x}^{\mathrm{3}} \:+\mathrm{1}\right)^{\mathrm{2}} \:\:{e}^{−{x}^{\mathrm{6}} \:−\mathrm{2}{x}^{\mathrm{3}} } {dx}\:.{ch}.{x}^{\mathrm{3}} \:={t} \\ $$$${give}\:\:{I}\:=\int_{−\infty} ^{+\infty} \:\:\left({t}+\mathrm{1}\right)^{\mathrm{2}} \:{e}^{−{t}^{\mathrm{2}} −\mathrm{2}{t}} \:{dt} \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \left({t}+\mathrm{1}\right)\left(−\mathrm{2}{t}−\mathrm{2}\right){e}^{−{t}^{\mathrm{2}} \:−\mathrm{2}{t}} {dt}\:\left({by}\:{parts}\right) \\ $$$$−\mathrm{2}{I}\:\:=\:\left[\left({t}+\mathrm{1}\right){e}^{−{t}^{\mathrm{2}} −\mathrm{2}{t}} \right]_{−\infty} ^{+\infty} \:\:−\int_{−\infty} ^{+\infty} \:{e}^{−{t}^{\mathrm{2}} \:−\mathrm{2}{t}} {dt}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:\:=\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left(\:\:\left({t}+\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{1}\right)} {dt}\:\:=\:{e}\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \:{dt} \\ $$$$=_{{t}+\mathrm{1}={x}} \:{e}\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{x}^{\mathrm{2}} } {dx}\:=\:{e}\:\sqrt{\pi\:}\:\Rightarrow\:{I}\:=\:\frac{{e}\sqrt{\pi}}{\mathrm{2}}\: \\ $$$${brcause}\:\:\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } \:{dx}=\sqrt{\pi}\:. \\ $$
Commented by Joel578 last updated on 13/Apr/18
$${Thank}\:{you}\:{very}\:{much} \\ $$
Commented by abdo imad last updated on 13/Apr/18
$${nevermind}\:\:{sir}\:{joel}. \\ $$
