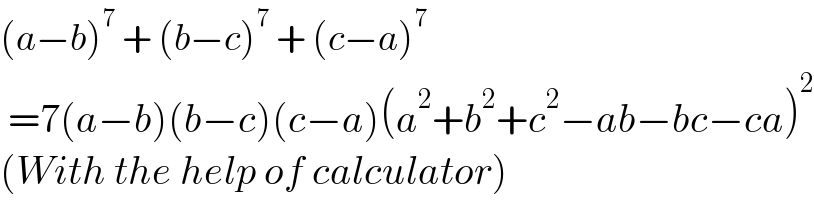Menu Close

evaluate-a-b-7-b-c-7-c-a-7-a-b-3-b-c-3-c-a-3-a-2-b-2-c-2-ab-bc-ca-

Tinku Tara 0 Comments
Pin




Question Number 171642 by infinityaction last updated on 19/Jun/22
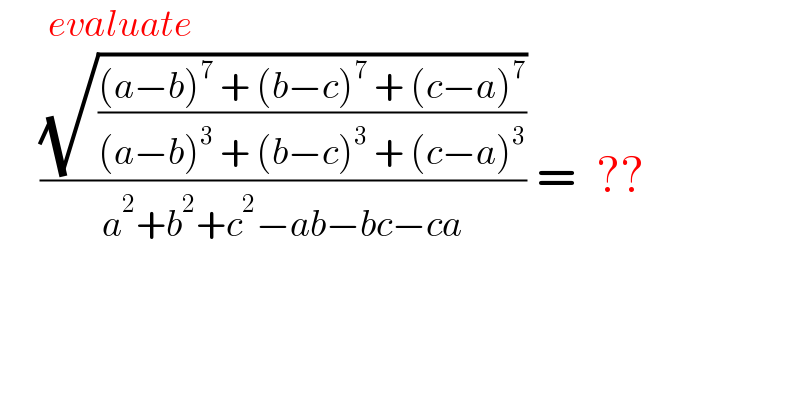
evaluate ((√(((a−b)^7 + (b−c)^7 + (c−a)^7 )/((a−b)^3 + (b−c)^3 + (c−a)^3 )))/(a^2 +b^2 +c^2 −ab−bc−ca)) = ??
evaluate(a−b)7+(b−c)7+(c−a)7(a−b)3+(b−c)3+(c−a)3a2+b2+c2−ab−bc−ca=??
Commented by infinityaction last updated on 19/Jun/22
let a−b = 𝛂 , b−c = 𝛃 , c−a = 𝛄 𝛂+𝛃+𝛄 = Σα = 0 𝛂^3 +𝛃^3 +𝛄^3 = Σα^3 = 3𝛂𝛃𝛄 then x^3 +(𝛂𝛃+𝛃𝛄+𝛄𝛂)x−𝛂𝛃𝛄 = 0 this equations has roots 𝛂 ,𝛃 ,𝛄 αβγ = P and αβ+βγ+γα = Q x^3 = P− Qx x^7 = Px.x^3 − Qx^2 .x^3 x^7 = Px(P−Qx)−x^2 Q(P−Qx) x^7 = P^2 x − PQx^2 −PQx^2 +Q^2 x^3 x^7 = P^2 x−2PQx^2 +Q^2 x^3 𝛂^(7 ) +𝛃^7 +𝛄^7 = P 𝚺𝛂 −2PQ 𝚺𝛂^2 + Q^2 𝚺𝛂^3 𝚺𝛂^7 = 3PQ^(2 ) −2PQ{ (𝚺𝛂)^2 −2𝚺𝛂𝛃 } 𝚺𝛂^7 = 3PQ^2 −2PQ(−2Q) 𝚺𝛂^(7 ) = 7PQ^2 and 𝚺𝛂^3 = 3P ((𝚺𝛂^7 )/(𝚺𝛂^3 )) = (7/3)Q a^2 +b^2 +c^2 −ab−bc−ca = (1/2)[(a−b)^2 +(b−c)^2 +(c−a)^2 ] a^2 +b^2 +c^2 −ab−bc−ca = (1/2){𝛂^2 +𝛃^2 +𝛄^2 } a^2 +b^2 +c^2 −ab−bc−ca = (1/2){−2Q}= −Q so ∣ ((√((7/3)Q^2 ))/(−Q)) ∣= ∣(((√((7/3) ))Q)/(−Q))∣ = (√(7/3))
\boldsymbollet\boldsymbola−\boldsymbolb=\boldsymbolα,\boldsymbolb−\boldsymbolc=\boldsymbolβ,\boldsymbolc−\boldsymbola=\boldsymbolγ\boldsymbolα+\boldsymbolβ+\boldsymbolγ=Σα=0\boldsymbolα3+\boldsymbolβ3+\boldsymbolγ3=Σα3=3\boldsymbolαβγthen\boldsymbolx3+(\boldsymbolαβ+\boldsymbolβγ+\boldsymbolγα)\boldsymbolx−\boldsymbolαβγ=0\boldsymbolthis\boldsymbolequations\boldsymbolhas\boldsymbolroots\boldsymbolα,\boldsymbolβ,\boldsymbolγαβγ=Pandαβ+βγ+γα=Q\boldsymbolx3=P−Qx\boldsymbolx7=\boldsymbolPx.\boldsymbolx3−\boldsymbolQx2.\boldsymbolx3\boldsymbolx7=\boldsymbolPx(\boldsymbolP−\boldsymbolQx)−\boldsymbolx2\boldsymbolQ(\boldsymbolP−\boldsymbolQx)\boldsymbolx7=\boldsymbolP2\boldsymbolx−\boldsymbolPQx2−\boldsymbolPQx2+\boldsymbolQ2\boldsymbolx3\boldsymbolx7=\boldsymbolP2\boldsymbolx−2\boldsymbolPQx2+\boldsymbolQ2\boldsymbolx3\boldsymbolα7+\boldsymbolβ7+\boldsymbolγ7=\boldsymbolP\boldsymbolΣα−2\boldsymbolPQ\boldsymbolΣα2+\boldsymbolQ2\boldsymbolΣα3\boldsymbolΣα7=3\boldsymbolPQ2−2\boldsymbolPQ{(\boldsymbolΣα)2−2\boldsymbolΣαβ}\boldsymbolΣα7=3\boldsymbolPQ2−2\boldsymbolPQ(−2\boldsymbolQ)\boldsymbolΣα7=7\boldsymbolPQ2\boldsymboland\boldsymbolΣα3=3\boldsymbolP\boldsymbolΣα7\boldsymbolΣα3=73\boldsymbolQ\boldsymbola2+\boldsymbolb2+\boldsymbolc2−\boldsymbolab−\boldsymbolbc−\boldsymbolca=12[(\boldsymbola−\boldsymbolb)2+(\boldsymbolb−\boldsymbolc)2+(\boldsymbolc−\boldsymbola)2]\boldsymbola2+\boldsymbolb2+\boldsymbolc2−\boldsymbolab−\boldsymbolbc−\boldsymbolca=12{\boldsymbolα2+\boldsymbolβ2+\boldsymbolγ2}\boldsymbola2+\boldsymbolb2+\boldsymbolc2−\boldsymbolab−\boldsymbolbc−\boldsymbolca=12{−2\boldsymbolQ}=−\boldsymbolQso∣73\boldsymbolQ2−\boldsymbolQ∣=∣73\boldsymbolQ−\boldsymbolQ∣=73
Commented by Rasheed.Sindhi last updated on 19/Jun/22
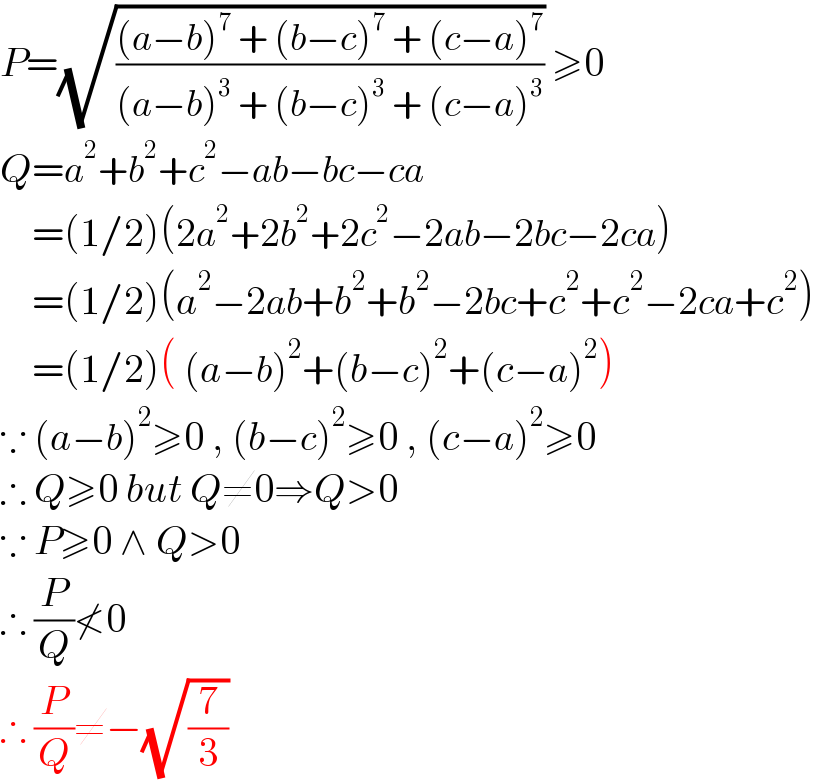
P=(√(((a−b)^7 + (b−c)^7 + (c−a)^7 )/((a−b)^3 + (b−c)^3 + (c−a)^3 ))) ≥0 Q=a^2 +b^2 +c^2 −ab−bc−ca =(1/2)(2a^2 +2b^2 +2c^2 −2ab−2bc−2ca) =(1/2)(a^2 −2ab+b^2 +b^2 −2bc+c^2 +c^2 −2ca+c^2 ) =(1/2)( (a−b)^2 +(b−c)^2 +(c−a)^2 ) ∵ (a−b)^2 ≥0 , (b−c)^2 ≥0 , (c−a)^2 ≥0 ∴ Q≥0 but Q≠0⇒Q>0 ∵ P≥0 ∧ Q>0 ∴ (P/Q)≮0 ∴ (P/Q)≠−(√(7/3))
P=(a−b)7+(b−c)7+(c−a)7(a−b)3+(b−c)3+(c−a)3⩾0Q=a2+b2+c2−ab−bc−ca=(1/2)(2a2+2b2+2c2−2ab−2bc−2ca)=(1/2)(a2−2ab+b2+b2−2bc+c2+c2−2ca+c2)=(1/2)((a−b)2+(b−c)2+(c−a)2)∵(a−b)2⩾0,(b−c)2⩾0,(c−a)2⩾0∴Q⩾0butQ≠0⇒Q>0∵P⩾0∧Q>0∴PQ≮0∴PQ≠−73
Commented by infinityaction last updated on 19/Jun/22
got it sir thanks
gotitsirthanks
Commented by Rasheed.Sindhi last updated on 19/Jun/22
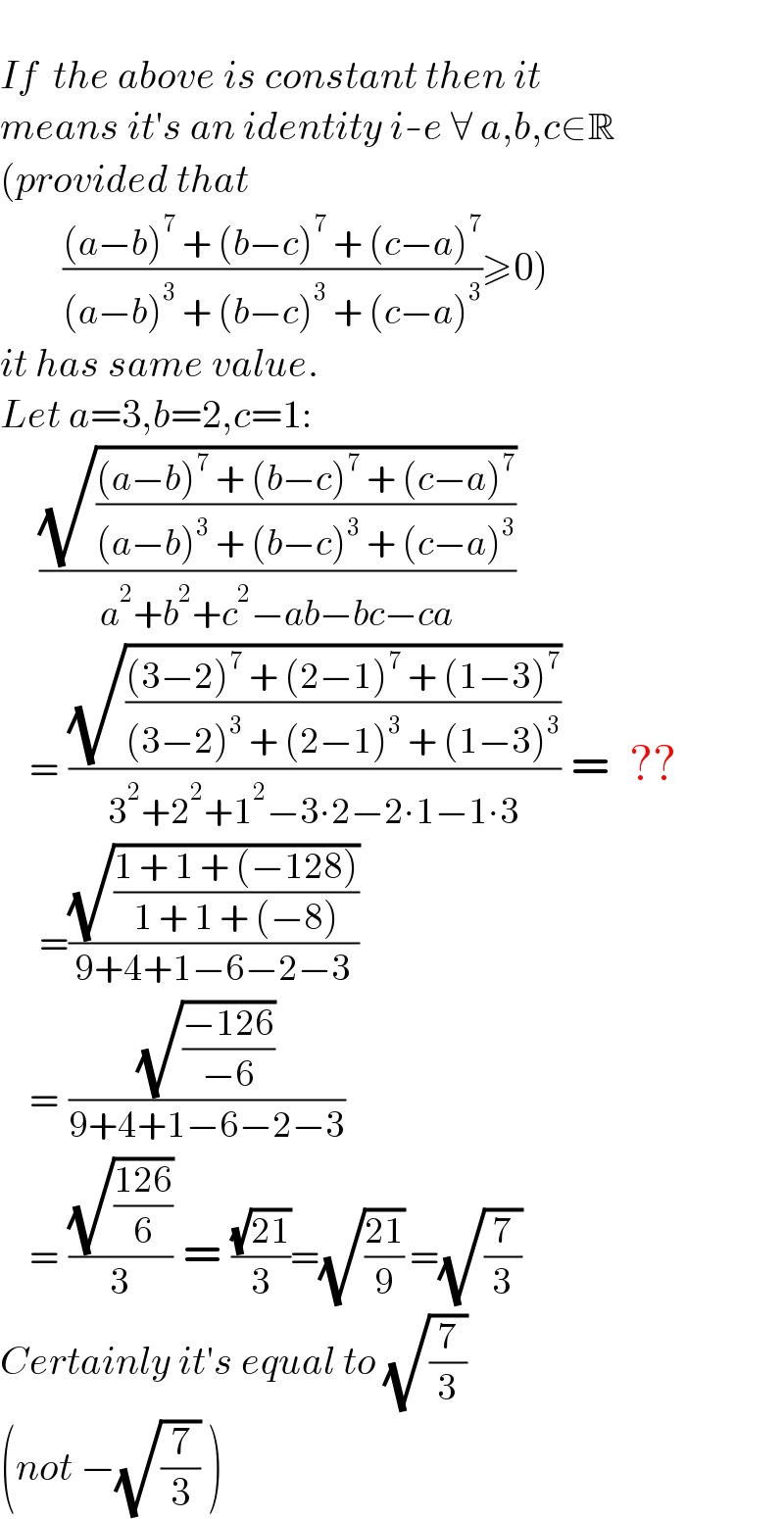
If the above is constant then it means it′s an identity i-e ∀ a,b,c∈R (provided that (((a−b)^7 + (b−c)^7 + (c−a)^7 )/((a−b)^3 + (b−c)^3 + (c−a)^3 ))≥0) it has same value. Let a=3,b=2,c=1: ((√(((a−b)^7 + (b−c)^7 + (c−a)^7 )/((a−b)^3 + (b−c)^3 + (c−a)^3 )))/(a^2 +b^2 +c^2 −ab−bc−ca)) = ((√(((3−2)^7 + (2−1)^7 + (1−3)^7 )/((3−2)^3 + (2−1)^3 + (1−3)^3 )))/(3^2 +2^2 +1^2 −3∙2−2∙1−1∙3)) = ?? =((√((1 + 1 + (−128))/(1 + 1 + (−8))))/(9+4+1−6−2−3)) = ((√((−126)/(−6)))/(9+4+1−6−2−3)) = ((√((126)/6))/3) = ((√(21))/3)=(√((21)/9)) =(√(7/3)) Certainly it′s equal to (√(7/3)) (not −(√(7/3)) )
Iftheaboveisconstantthenitmeansit′sanidentityi−e∀a,b,c∈R(providedthat(a−b)7+(b−c)7+(c−a)7(a−b)3+(b−c)3+(c−a)3⩾0)ithassamevalue.Leta=3,b=2,c=1:(a−b)7+(b−c)7+(c−a)7(a−b)3+(b−c)3+(c−a)3a2+b2+c2−ab−bc−ca=(3−2)7+(2−1)7+(1−3)7(3−2)3+(2−1)3+(1−3)332+22+12−3⋅2−2⋅1−1⋅3=??=1+1+(−128)1+1+(−8)9+4+1−6−2−3=−126−69+4+1−6−2−3=12663=213=219=73Certainlyit′sequalto73(not−73)
Commented by Tawa11 last updated on 25/Jun/22
Great sir
Greatsir
Answered by Rasheed.Sindhi last updated on 19/Jun/22
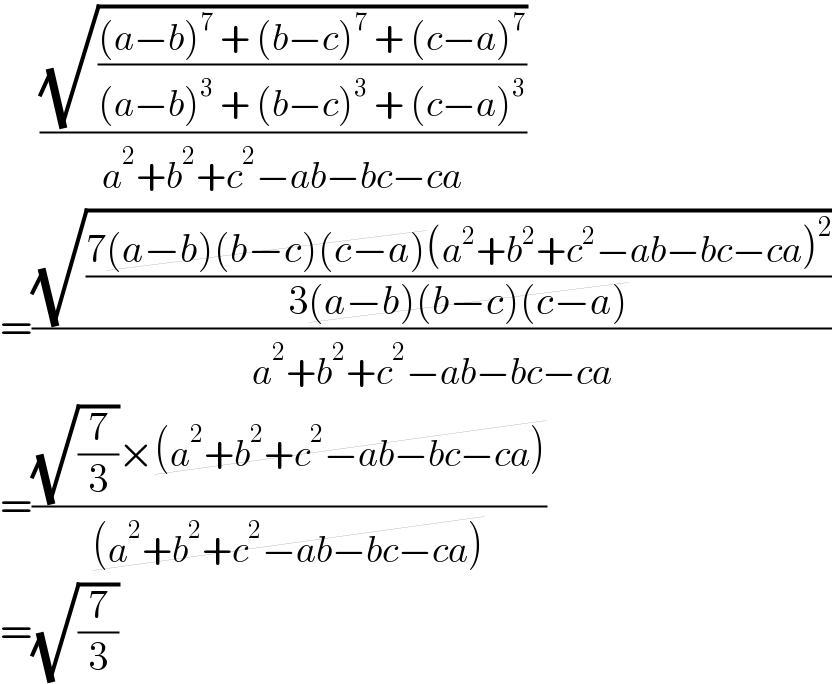
((√(((a−b)^7 + (b−c)^7 + (c−a)^7 )/((a−b)^3 + (b−c)^3 + (c−a)^3 )))/(a^2 +b^2 +c^2 −ab−bc−ca)) =((√((7(a−b)(b−c)(c−a)(a^2 +b^2 +c^2 −ab−bc−ca)^2 )/(3(a−b)(b−c)(c−a))))/(a^2 +b^2 +c^2 −ab−bc−ca)) =(((√(7/3))×(a^2 +b^2 +c^2 −ab−bc−ca))/((a^2 +b^2 +c^2 −ab−bc−ca))) =(√(7/3))
(a−b)7+(b−c)7+(c−a)7(a−b)3+(b−c)3+(c−a)3a2+b2+c2−ab−bc−ca=7\cancel(a−b)(b−c)(c−a)(a2+b2+c2−ab−bc−ca)23\cancel(a−b)(b−c)(c−a)a2+b2+c2−ab−bc−ca=73×\cancel(a2+b2+c2−ab−bc−ca)\cancel(a2+b2+c2−ab−bc−ca)=73
Commented by infinityaction last updated on 19/Jun/22
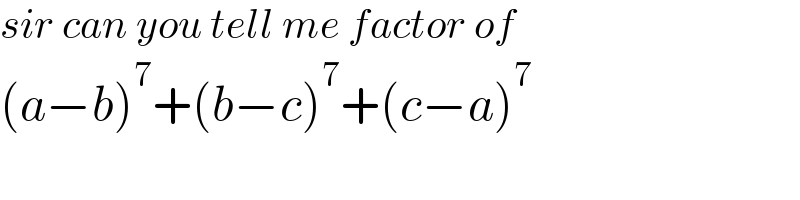
sir can you tell me factor of (a−b)^7 +(b−c)^7 +(c−a)^7
sircanyoutellmefactorof(a−b)7+(b−c)7+(c−a)7
Commented by Rasheed.Sindhi last updated on 19/Jun/22
(a−b)^7 + (b−c)^7 + (c−a)^7 =7(a−b)(b−c)(c−a)(a^2 +b^2 +c^2 −ab−bc−ca)^2 (With the help of calculator)
(a−b)7+(b−c)7+(c−a)7=7(a−b)(b−c)(c−a)(a2+b2+c2−ab−bc−ca)2(Withthehelpofcalculator)

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *