Question Number 168978 by MikeH last updated on 22/Apr/22
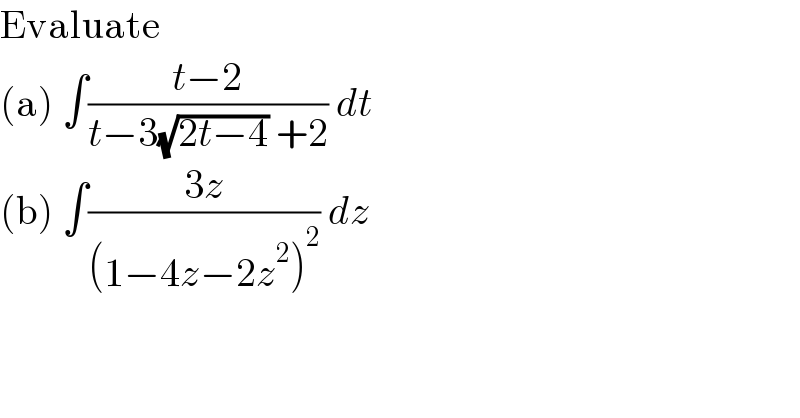
$$\mathrm{Evaluate}\: \\ $$$$\left(\mathrm{a}\right)\:\int\frac{{t}−\mathrm{2}}{{t}−\mathrm{3}\sqrt{\mathrm{2}{t}−\mathrm{4}}\:+\mathrm{2}}\:{dt}\: \\ $$$$\left(\mathrm{b}\right)\:\int\frac{\mathrm{3}{z}}{\left(\mathrm{1}−\mathrm{4}{z}−\mathrm{2}{z}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dz} \\ $$
Answered by floor(10²Eta[1]) last updated on 22/Apr/22

$$\left(\mathrm{a}\right): \\ $$$$\sqrt{\mathrm{2t}−\mathrm{4}}=\mathrm{u}\Rightarrow\mathrm{dt}=\mathrm{udu},\:\mathrm{t}=\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2} \\ $$$$\int\frac{\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{2}}}{\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{4}−\mathrm{3u}}\mathrm{du}=\int\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{u}^{\mathrm{2}} −\mathrm{6u}+\mathrm{8}}\mathrm{du} \\ $$$$=\int\left(\mathrm{u}+\mathrm{6}\right)\mathrm{du}+\int\frac{\mathrm{28u}−\mathrm{48}}{\mathrm{u}^{\mathrm{2}} −\mathrm{6u}+\mathrm{8}} \\ $$$$\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{6u}+\int\frac{\mathrm{28u}−\mathrm{48}}{\left(\mathrm{u}−\mathrm{2}\right)\left(\mathrm{u}−\mathrm{4}\right)}\mathrm{du} \\ $$$$\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{6u}−\mathrm{4}\int\frac{\mathrm{du}}{\mathrm{u}−\mathrm{2}}+\mathrm{32}\int\frac{\mathrm{du}}{\mathrm{u}−\mathrm{4}} \\ $$$$\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{6u}−\mathrm{4ln}\mid\mathrm{u}−\mathrm{2}\mid+\mathrm{32ln}\mid\mathrm{u}−\mathrm{4}\mid+\mathrm{C} \\ $$$$\mathrm{t}−\mathrm{2}+\mathrm{6}\sqrt{\mathrm{2t}−\mathrm{4}}−\mathrm{4ln}\mid\sqrt{\mathrm{2t}−\mathrm{4}}−\mathrm{2}\mid+\mathrm{32ln}\mid\sqrt{\mathrm{2t}−\mathrm{4}}−\mathrm{4}\mid+\mathrm{C} \\ $$
