Menu Close

evaluate-cos-2x-sin-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 32156 by jarjum last updated on 20/Mar/18
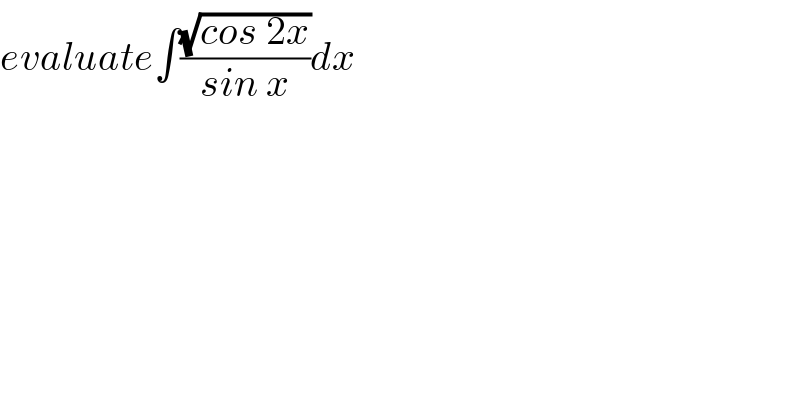
evaluate∫((√(cos 2x))/(sin x))dx
$${evaluate}\int\frac{\sqrt{{cos}\:\mathrm{2}{x}}}{{sin}\:{x}}{dx} \\ $$
Commented by abdo imad last updated on 20/Mar/18
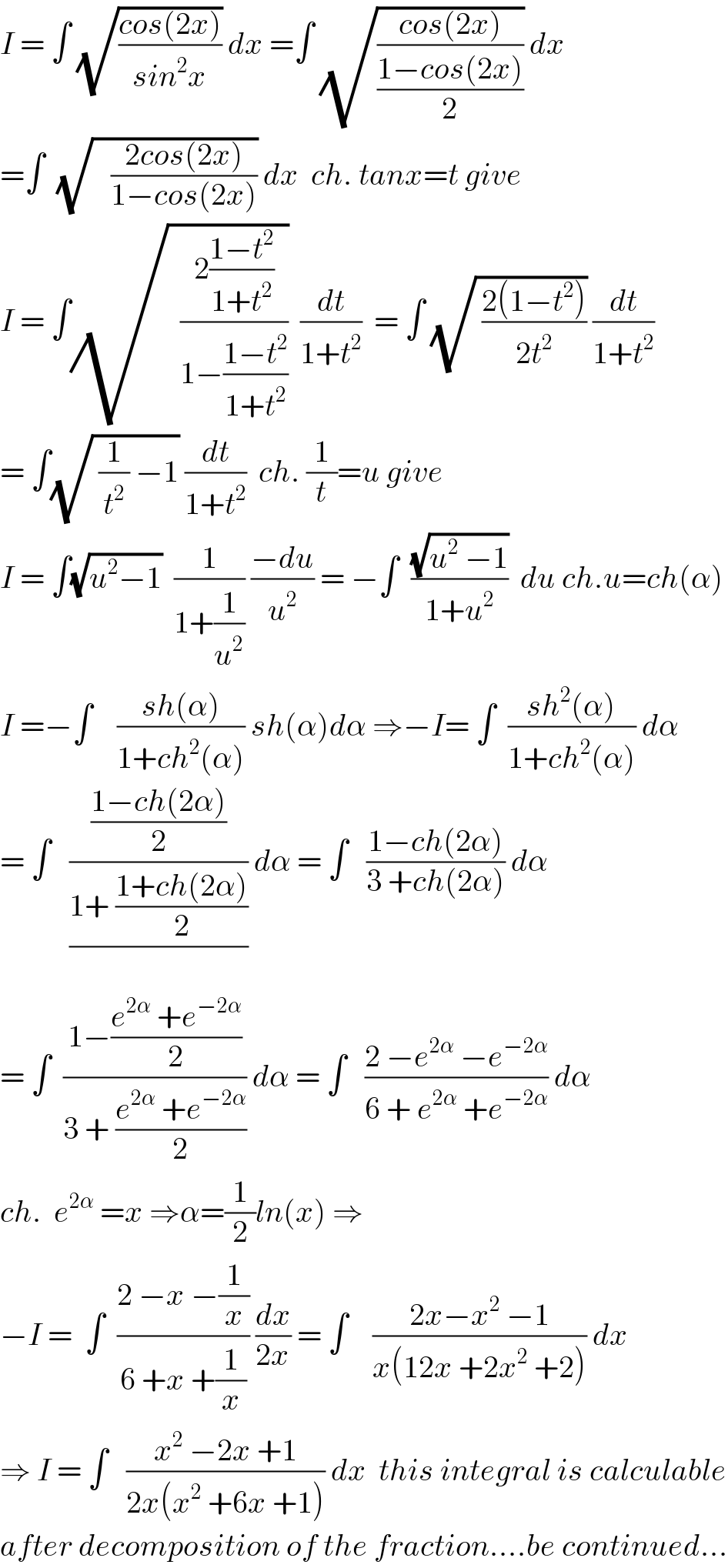
I = ∫ (√((cos(2x))/(sin^2 x))) dx =∫ (√((cos(2x))/((1−cos(2x))/2))) dx =∫ (√( ((2cos(2x))/(1−cos(2x))))) dx ch. tanx=t give I = ∫(√( ((2((1−t^2 )/(1+t^2 )))/(1−((1−t^2 )/(1+t^2 )))))) (dt/(1+t^2 )) = ∫ (√( ((2(1−t^2 ))/(2t^2 )))) (dt/(1+t^2 )) = ∫(√( (1/t^2 ) −1)) (dt/(1+t^2 )) ch. (1/t)=u give I = ∫(√(u^2 −1)) (1/(1+(1/u^2 ))) ((−du)/u^2 ) = −∫ ((√(u^2 −1))/(1+u^2 )) du ch.u=ch(α) I =−∫ ((sh(α))/(1+ch^2 (α))) sh(α)dα ⇒−I= ∫ ((sh^2 (α))/(1+ch^2 (α))) dα = ∫ (((1−ch(2α))/2)/((1+ ((1+ch(2α))/2))/)) dα = ∫ ((1−ch(2α))/(3 +ch(2α))) dα = ∫ ((1−((e^(2α) +e^(−2α) )/2))/(3 + ((e^(2α) +e^(−2α) )/2))) dα = ∫ ((2 −e^(2α) −e^(−2α) )/(6 + e^(2α) +e^(−2α) )) dα ch. e^(2α) =x ⇒α=(1/2)ln(x) ⇒ −I = ∫ ((2 −x −(1/x))/(6 +x +(1/x))) (dx/(2x)) = ∫ ((2x−x^2 −1)/(x(12x +2x^2 +2))) dx ⇒ I = ∫ ((x^2 −2x +1)/(2x(x^2 +6x +1))) dx this integral is calculable after decomposition of the fraction....be continued...
$${I}\:=\:\int\:\sqrt{\frac{{cos}\left(\mathrm{2}{x}\right)}{{sin}^{\mathrm{2}} {x}}}\:{dx}\:=\int\:\sqrt{\frac{{cos}\left(\mathrm{2}{x}\right)}{\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}}}\:{dx} \\ $$$$=\int\:\:\sqrt{\:\:\:\frac{\mathrm{2}{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}}\:{dx}\:\:{ch}.\:{tanx}={t}\:{give} \\ $$$${I}\:=\:\int\sqrt{\:\:\frac{\mathrm{2}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}}\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:=\:\int\:\sqrt{\:\frac{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{2}{t}^{\mathrm{2}} }}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int\sqrt{\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:−\mathrm{1}}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{ch}.\:\frac{\mathrm{1}}{{t}}={u}\:{give} \\ $$$${I}\:=\:\int\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}\:\frac{−{du}}{{u}^{\mathrm{2}} }\:=\:−\int\:\:\frac{\sqrt{{u}^{\mathrm{2}} \:−\mathrm{1}}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\:{du}\:{ch}.{u}={ch}\left(\alpha\right) \\ $$$${I}\:=−\int\:\:\:\:\frac{{sh}\left(\alpha\right)}{\mathrm{1}+{ch}^{\mathrm{2}} \left(\alpha\right)}\:{sh}\left(\alpha\right){d}\alpha\:\Rightarrow−{I}=\:\int\:\:\frac{{sh}^{\mathrm{2}} \left(\alpha\right)}{\mathrm{1}+{ch}^{\mathrm{2}} \left(\alpha\right)}\:{d}\alpha \\ $$$$=\:\int\:\:\:\frac{\frac{\mathrm{1}−{ch}\left(\mathrm{2}\alpha\right)}{\mathrm{2}}}{\frac{\mathrm{1}+\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}\alpha\right)}{\mathrm{2}}}{}}\:{d}\alpha\:=\:\int\:\:\:\frac{\mathrm{1}−{ch}\left(\mathrm{2}\alpha\right)}{\mathrm{3}\:+{ch}\left(\mathrm{2}\alpha\right)}\:{d}\alpha \\ $$$$=\:\int\:\:\frac{\mathrm{1}−\frac{{e}^{\mathrm{2}\alpha} \:+{e}^{−\mathrm{2}\alpha} }{\mathrm{2}}}{\mathrm{3}\:+\:\frac{{e}^{\mathrm{2}\alpha} \:+{e}^{−\mathrm{2}\alpha} }{\mathrm{2}}}\:{d}\alpha\:=\:\int\:\:\:\frac{\mathrm{2}\:−{e}^{\mathrm{2}\alpha} \:−{e}^{−\mathrm{2}\alpha} }{\mathrm{6}\:+\:{e}^{\mathrm{2}\alpha} \:+{e}^{−\mathrm{2}\alpha} }\:{d}\alpha \\ $$$${ch}.\:\:{e}^{\mathrm{2}\alpha} \:={x}\:\Rightarrow\alpha=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}\right)\:\Rightarrow \\ $$$$−{I}\:=\:\:\int\:\:\frac{\mathrm{2}\:−{x}\:−\frac{\mathrm{1}}{{x}}}{\mathrm{6}\:+{x}\:+\frac{\mathrm{1}}{{x}}}\:\frac{{dx}}{\mathrm{2}{x}}\:=\:\int\:\:\:\:\frac{\mathrm{2}{x}−{x}^{\mathrm{2}} \:−\mathrm{1}}{{x}\left(\mathrm{12}{x}\:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}\right)}\:{dx} \\ $$$$\Rightarrow\:{I}\:=\:\int\:\:\:\frac{{x}^{\mathrm{2}} \:−\mathrm{2}{x}\:+\mathrm{1}}{\mathrm{2}{x}\left({x}^{\mathrm{2}} \:+\mathrm{6}{x}\:+\mathrm{1}\right)}\:{dx}\:\:{this}\:{integral}\:{is}\:{calculable} \\ $$$${after}\:{decomposition}\:{of}\:{the}\:{fraction}….{be}\:{continued}… \\ $$
Commented by jarjum last updated on 21/Mar/18
thank you
$${thank}\:{you}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *