Question Number 102001 by hardylanes last updated on 06/Jul/20
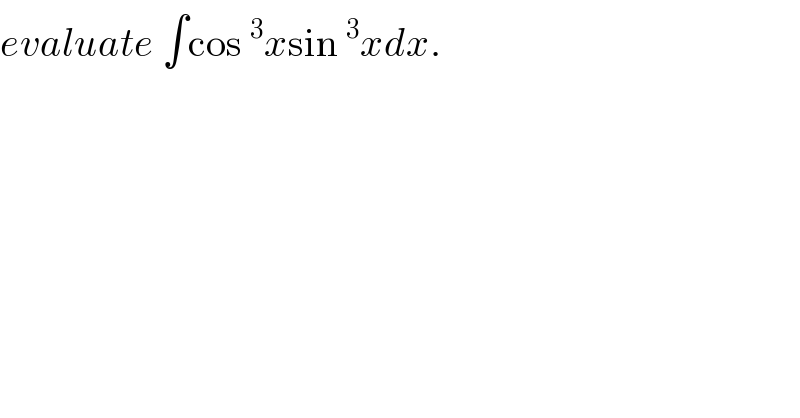
$${evaluate}\:\int\mathrm{cos}\:^{\mathrm{3}} {x}\mathrm{sin}\:^{\mathrm{3}} {xdx}. \\ $$
Answered by bobhans last updated on 06/Jul/20
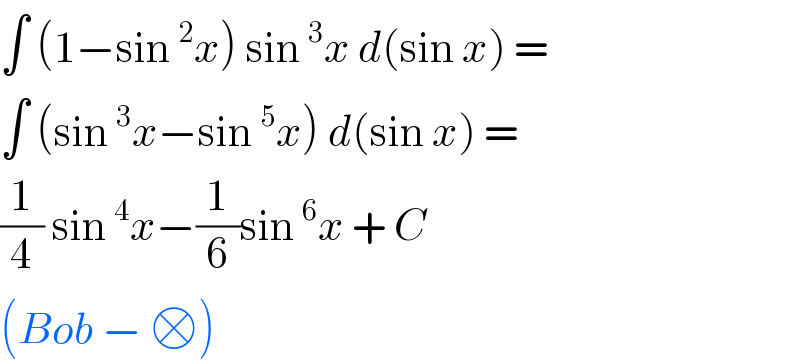
$$\int\:\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)\:\mathrm{sin}\:^{\mathrm{3}} {x}\:{d}\left(\mathrm{sin}\:{x}\right)\:=\: \\ $$$$\int\:\left(\mathrm{sin}\:^{\mathrm{3}} {x}−\mathrm{sin}\:^{\mathrm{5}} {x}\right)\:{d}\left(\mathrm{sin}\:{x}\right)\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{sin}\:^{\mathrm{4}} {x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sin}\:^{\mathrm{6}} {x}\:+\:{C} \\ $$$$\left({Bob}\:−\:\square\right) \\ $$
Commented by hardylanes last updated on 06/Jul/20
that's it??
Commented by bobhans last updated on 06/Jul/20

$${what}? \\ $$
Answered by bobhans last updated on 06/Jul/20
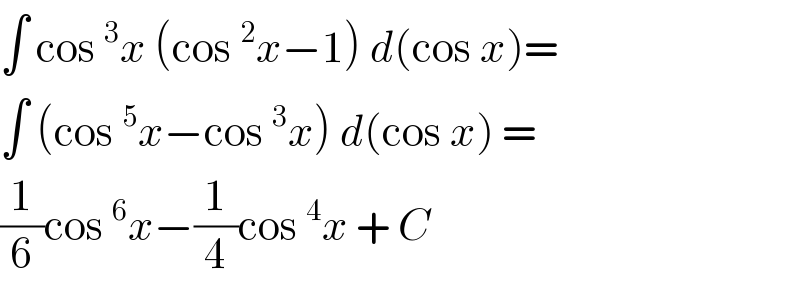
$$\int\:\mathrm{cos}\:^{\mathrm{3}} {x}\:\left(\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{1}\right)\:{d}\left(\mathrm{cos}\:{x}\right)= \\ $$$$\int\:\left(\mathrm{cos}\:^{\mathrm{5}} {x}−\mathrm{cos}\:^{\mathrm{3}} {x}\right)\:{d}\left(\mathrm{cos}\:{x}\right)\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cos}\:^{\mathrm{6}} {x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:^{\mathrm{4}} {x}\:+\:{C} \\ $$
