Menu Close

evaluate-dx-a-sin-x-b-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 83691 by niroj last updated on 05/Mar/20
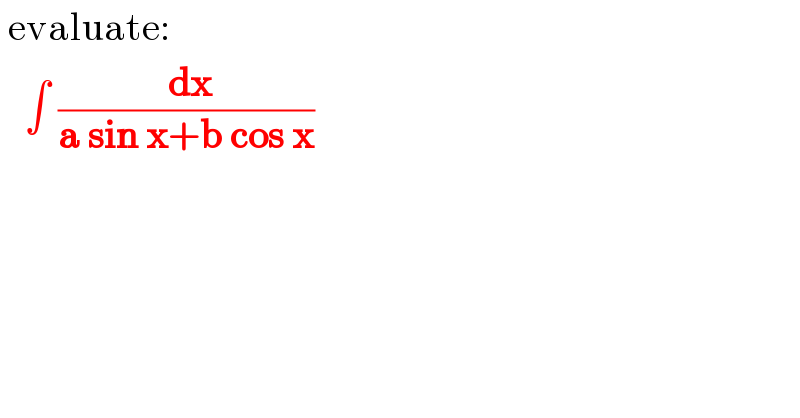
evaluate: ∫ (( dx)/(a sin x+b cos x))
$$\:\mathrm{evaluate}: \\ $$$$\:\:\:\int\:\frac{\:\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{b}}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{x}}} \\ $$
Commented by mathmax by abdo last updated on 05/Mar/20
we use changement tan((x/2))=t ⇒ I =∫ (1/(a((2t)/(1+t^2 )) +b((1−t^2 )/(1+t^2 ))))×((2dt)/(1+t^2 )) =2∫ (dt/(2at+b−bt^2 )) =−2∫ (dt/(bt^2 −2at −b)) Δ^′ =a^2 +b^2 >0 ⇒t_1 =((a+(√(a^2 +b^2 )))/b) and t_2 =((a−(√(a^2 +b^2 )))/b) ⇒ I =−2 ∫ (dt/(b(t−t_1 )(t−t_2 ))) =((−2)/(b(t_1 −t_2 )))∫ ((1/(t−t_1 ))−(1/(t−t_2 )))dt =((−2)/(b×((2(√(a^2 +b^2 )))/b))) ln∣((t−t_1 )/(t−t_2 ))∣ +C=((−1)/( (√(a^2 +b^2 ))))ln∣((tan((x/2))−((a+(√(a^2 +b^2 )))/b))/(tan((x/2))−((a−(√(a^2 +b^2 )))/b)))∣ +C =((−1)/( (√(a^2 +b^2 ))))ln∣((btan((x/2))−a−(√(a^2 +b^2 )))/(btan((x/2))−a+(√(a^2 +b^2 ))))∣ +C
$${we}\:{use}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:\Rightarrow \\ $$$${I}\:=\int\:\:\:\:\frac{\mathrm{1}}{{a}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+{b}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\int\:\:\:\:\frac{{dt}}{\mathrm{2}{at}+{b}−{bt}^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\int\:\:\:\frac{{dt}}{{bt}^{\mathrm{2}} −\mathrm{2}{at}\:−{b}} \\ $$$$\Delta^{'} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow{t}_{\mathrm{1}} =\frac{{a}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{{a}−\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}{{b}}\:\Rightarrow \\ $$$${I}\:=−\mathrm{2}\:\int\:\:\:\frac{{dt}}{{b}\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)}\:=\frac{−\mathrm{2}}{{b}\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)}\int\:\:\left(\frac{\mathrm{1}}{{t}−{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{{t}−{t}_{\mathrm{2}} }\right){dt} \\ $$$$=\frac{−\mathrm{2}}{{b}×\frac{\mathrm{2}\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}{{b}}}\:{ln}\mid\frac{{t}−{t}_{\mathrm{1}} }{{t}−{t}_{\mathrm{2}} }\mid\:+{C}=\frac{−\mathrm{1}}{\:\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}{ln}\mid\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\frac{{a}+\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}{{b}}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\frac{{a}−\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}}}\mid\:+{C} \\ $$$$=\frac{−\mathrm{1}}{\:\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}{ln}\mid\frac{{btan}\left(\frac{{x}}{\mathrm{2}}\right)−{a}−\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}{{btan}\left(\frac{{x}}{\mathrm{2}}\right)−{a}+\sqrt{{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }}\mid\:+{C} \\ $$
Commented by john santu last updated on 06/Mar/20
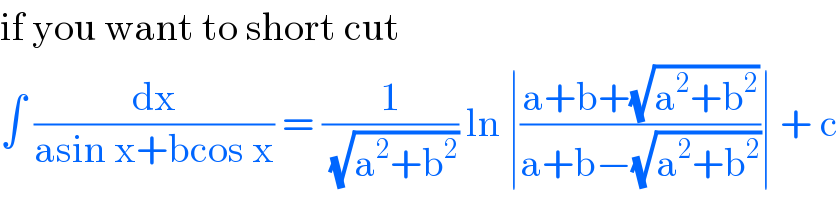
if you want to short cut ∫ (dx/(asin x+bcos x)) = (1/( (√(a^2 +b^2 )))) ln ∣((a+b+(√(a^2 +b^2 )))/(a+b−(√(a^2 +b^2 ))))∣ + c
$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{short}\:\mathrm{cut}\: \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{asin}\:\mathrm{x}+\mathrm{bcos}\:\mathrm{x}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\:\mathrm{ln}\:\mid\frac{\mathrm{a}+\mathrm{b}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}{\mathrm{a}+\mathrm{b}−\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\mid\:+\:\mathrm{c} \\ $$
Answered by john santu last updated on 05/Mar/20
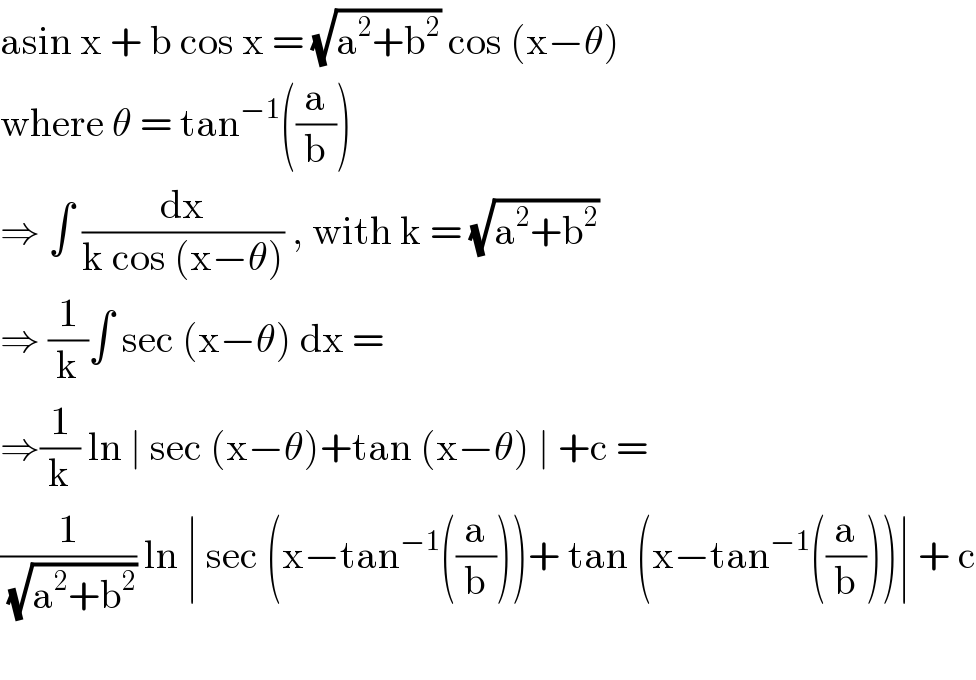
asin x + b cos x = (√(a^2 +b^2 )) cos (x−θ) where θ = tan^(−1) ((a/b)) ⇒ ∫ (dx/(k cos (x−θ))) , with k = (√(a^2 +b^2 )) ⇒ (1/k)∫ sec (x−θ) dx = ⇒(1/k) ln ∣ sec (x−θ)+tan (x−θ) ∣ +c = (1/( (√(a^2 +b^2 )))) ln ∣ sec (x−tan^(−1) ((a/b)))+ tan (x−tan^(−1) ((a/b)))∣ + c
$$\mathrm{asin}\:\mathrm{x}\:+\:\mathrm{b}\:\mathrm{cos}\:\mathrm{x}\:=\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\:\mathrm{cos}\:\left(\mathrm{x}−\theta\right)\: \\ $$$$\mathrm{where}\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{b}}\right) \\ $$$$\Rightarrow\:\int\:\frac{\mathrm{dx}}{\mathrm{k}\:\mathrm{cos}\:\left(\mathrm{x}−\theta\right)}\:,\:\mathrm{with}\:\mathrm{k}\:=\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{k}}\int\:\mathrm{sec}\:\left(\mathrm{x}−\theta\right)\:\mathrm{dx}\:= \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{k}}\:\mathrm{ln}\:\mid\:\mathrm{sec}\:\left(\mathrm{x}−\theta\right)+\mathrm{tan}\:\left(\mathrm{x}−\theta\right)\:\mid\:+\mathrm{c}\:= \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\:\mathrm{ln}\:\mid\:\mathrm{sec}\:\left(\mathrm{x}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{b}}\right)\right)+\:\mathrm{tan}\:\left(\mathrm{x}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{b}}\right)\right)\mid\:+\:\mathrm{c} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *