Question Number 144896 by physicstutes last updated on 30/Jun/21

$$\mathrm{Evaluate}\: \\ $$$$\:\int{e}^{{x}} \left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} {dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 30/Jun/21
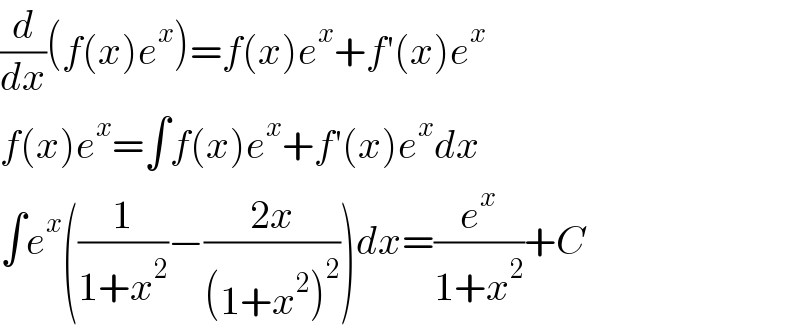
$$\frac{{d}}{{dx}}\left({f}\left({x}\right){e}^{{x}} \right)={f}\left({x}\right){e}^{{x}} +{f}'\left({x}\right){e}^{{x}} \\ $$$${f}\left({x}\right){e}^{{x}} =\int{f}\left({x}\right){e}^{{x}} +{f}'\left({x}\right){e}^{{x}} {dx} \\ $$$$\int{e}^{{x}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{\mathrm{2}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right){dx}=\frac{{e}^{{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }+{C} \\ $$
