Question Number 119831 by talminator2856791 last updated on 27/Oct/20
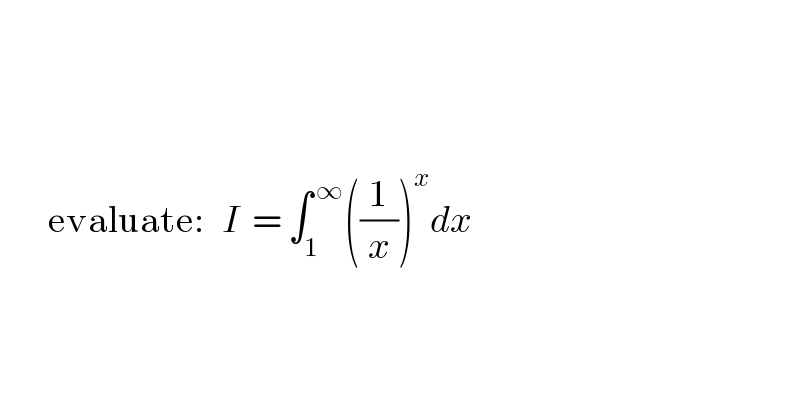
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{evaluate}:\:\:\:{I}\:\:=\:\int_{\mathrm{1}} ^{\:\infty} \left(\frac{\mathrm{1}}{{x}}\right)^{{x}} {dx} \\ $$$$\: \\ $$$$\: \\ $$
Commented by Dwaipayan Shikari last updated on 27/Oct/20

$${Generally} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{xlogx}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{xlogx}\right)^{{n}} }{{n}!} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {log}^{{n}} {x}\:{dx}\:\:\:\:\:\:\:\:\:\:\:\:{logx}={t}\Rightarrow\frac{\mathrm{1}}{{x}}=\frac{{dt}}{{dx}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!}\int_{\infty} ^{\mathrm{0}} {t}^{{n}} {e}^{\left({n}+\mathrm{1}\right){t}} {dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n}+\mathrm{1}\right){t}=−{u}\Rightarrow−\left({n}+\mathrm{1}\right)=\frac{{du}}{{dt}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}!\left({n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}} }.{e}^{−{u}} {du} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{2}{n}} \frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!\left({n}+\mathrm{1}\right)^{{n}} }\Gamma\left({n}+\mathrm{1}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}!\:\left(\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)!\left({n}+\mathrm{1}\right)^{{n}} } \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\left({n}+\mathrm{1}\right)} } \\ $$
