Question Number 28876 by Rasheed.Sindhi last updated on 31/Jan/18
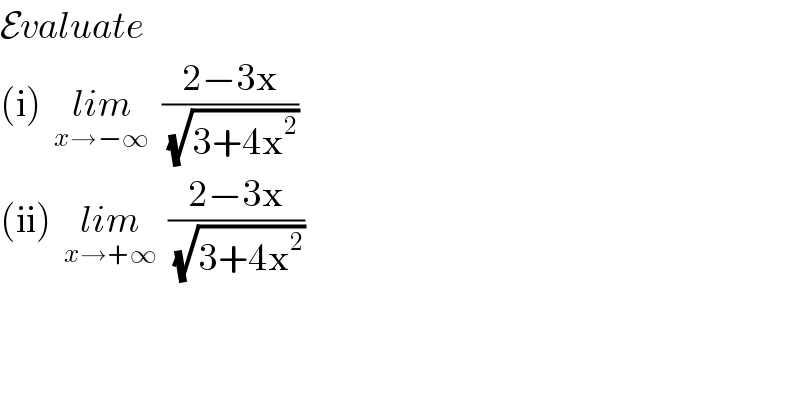
$$\mathcal{E}{valuate} \\ $$$$\left(\mathrm{i}\right)\:\:\underset{{x}\rightarrow−\infty} {{lim}}\:\:\frac{\mathrm{2}−\mathrm{3x}}{\:\sqrt{\mathrm{3}+\mathrm{4x}^{\mathrm{2}} }} \\ $$$$\left(\mathrm{ii}\right)\:\:\underset{{x}\rightarrow+\infty} {{lim}}\:\:\frac{\mathrm{2}−\mathrm{3x}}{\:\sqrt{\mathrm{3}+\mathrm{4x}^{\mathrm{2}} }} \\ $$
Commented by abdo imad last updated on 31/Jan/18
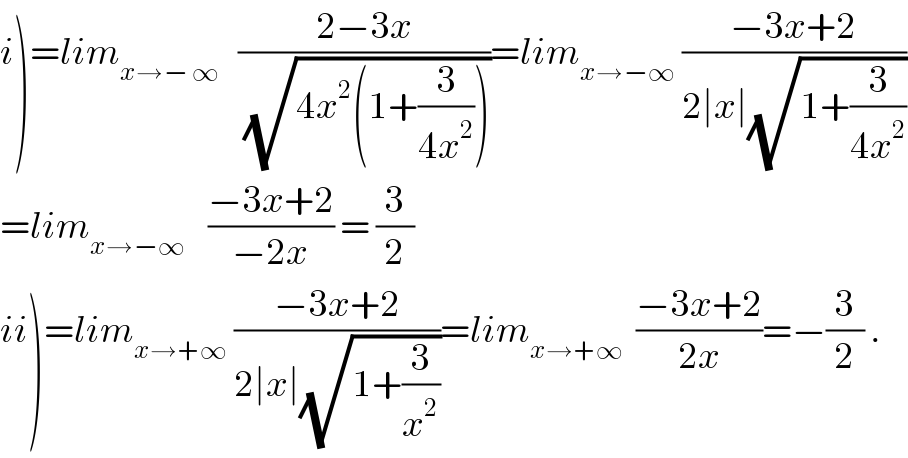
$$\left.{i}\right)={lim}_{{x}\rightarrow−\:\infty} \:\:\:\frac{\mathrm{2}−\mathrm{3}{x}}{\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} }\right)}}={lim}_{{x}\rightarrow−\infty} \:\frac{−\mathrm{3}{x}+\mathrm{2}}{\mathrm{2}\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} }}} \\ $$$$={lim}_{{x}\rightarrow−\infty\:} \:\:\:\frac{−\mathrm{3}{x}+\mathrm{2}}{−\mathrm{2}{x}}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left.{ii}\right)={lim}_{{x}\rightarrow+\infty} \:\frac{−\mathrm{3}{x}+\mathrm{2}}{\mathrm{2}\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{x}^{\mathrm{2}} }}}={lim}_{{x}\rightarrow+\infty} \:\:\frac{−\mathrm{3}{x}+\mathrm{2}}{\mathrm{2}{x}}=−\frac{\mathrm{3}}{\mathrm{2}}\:. \\ $$
