Question Number 121694 by bemath last updated on 11/Nov/20
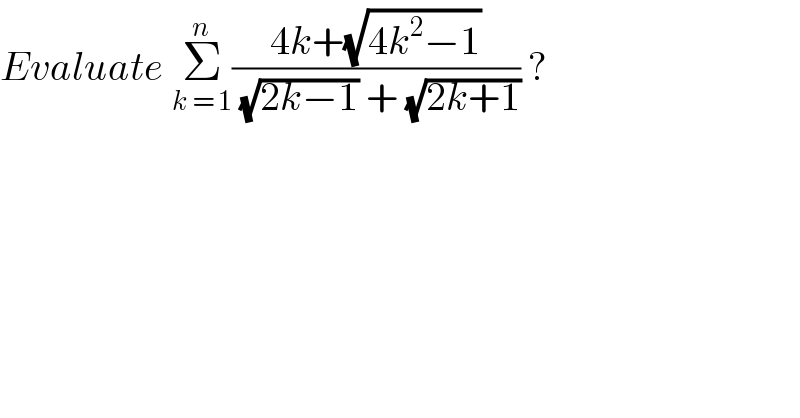
$${Evaluate}\:\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{4}{k}+\sqrt{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{\mathrm{2}{k}−\mathrm{1}}\:+\:\sqrt{\mathrm{2}{k}+\mathrm{1}}}\:? \\ $$
Answered by liberty last updated on 11/Nov/20
![let (√(2k−1)) = a and (√(2k+1)) = b ⇒ a^2 +b^2 = 4k ∧ ab = (√(4k^2 −1)) ⇒ ((4k+(√(4k^2 −1)))/( (√(2k−1)) + (√(2k+1)))) = ((a^2 +b^2 +ab)/(a+b)) ⇒ (((a^3 −b^3 )/(a−b))/(a+b)) = ((a^3 −b^3 )/(a^2 −b^2 )) = ((a^3 −b^3 )/(−2))= ((b^3 −a^3 )/2) . since a^2 −b^2 = (2k−1)−(2k+1)=−2 ⇒((4k+(√(4k^2 −1)))/( (√(2k−1)) + (√(2k+1)))) = (((√((2k+1)^3 ))−(√((2k−1)^3 )))/2) then Σ_(k = 1) ^n ((4k+(√(4k^2 −1)))/( (√(2k−1)) + (√(2k+1)))) = Σ_(k = 1) ^n (((√((2k+1)^3 ))−(√((2k−1)^3 )))/2) = (((√((2n+1)^3 ))−1)/2) . [ telescoping series ]](https://www.tinkutara.com/question/Q121695.png)
$$\:\mathrm{let}\:\sqrt{\mathrm{2k}−\mathrm{1}}\:=\:\mathrm{a}\:\mathrm{and}\:\sqrt{\mathrm{2k}+\mathrm{1}}\:=\:\mathrm{b}\: \\ $$$$\Rightarrow\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \:=\:\mathrm{4k}\:\wedge\:\mathrm{ab}\:=\:\sqrt{\mathrm{4k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow\:\frac{\mathrm{4k}+\sqrt{\mathrm{4k}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{\mathrm{2k}−\mathrm{1}}\:+\:\sqrt{\mathrm{2k}+\mathrm{1}}}\:=\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{ab}}{\mathrm{a}+\mathrm{b}} \\ $$$$\Rightarrow\:\frac{\frac{\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} }{\mathrm{a}−\mathrm{b}}}{\mathrm{a}+\mathrm{b}}\:=\:\frac{\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} }{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{a}^{\mathrm{3}} −\mathrm{b}^{\mathrm{3}} }{−\mathrm{2}}=\:\frac{\mathrm{b}^{\mathrm{3}} −\mathrm{a}^{\mathrm{3}} }{\mathrm{2}}\:.\:\mathrm{since}\:\: \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \:=\:\left(\mathrm{2k}−\mathrm{1}\right)−\left(\mathrm{2k}+\mathrm{1}\right)=−\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{4k}+\sqrt{\mathrm{4k}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{\mathrm{2k}−\mathrm{1}}\:+\:\sqrt{\mathrm{2k}+\mathrm{1}}}\:=\:\:\frac{\sqrt{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{3}} }−\sqrt{\left(\mathrm{2k}−\mathrm{1}\right)^{\mathrm{3}} }}{\mathrm{2}} \\ $$$$\mathrm{then}\:\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{4k}+\sqrt{\mathrm{4k}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{\mathrm{2k}−\mathrm{1}}\:+\:\sqrt{\mathrm{2k}+\mathrm{1}}}\:=\:\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\sqrt{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{3}} }−\sqrt{\left(\mathrm{2k}−\mathrm{1}\right)^{\mathrm{3}} }}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }−\mathrm{1}}{\mathrm{2}}\:.\:\left[\:\mathrm{telescoping}\:\mathrm{series}\:\right]\: \\ $$
